题目内容
如图，Rt△ABC的斜边AB=40cm，现将△ABC折叠，使点B与点A重合，折痕DE=15cm，则AD的长为
- A.20cm
- B.25cm
- C.55cm
- D.35cm
B
分析：根据折叠的性质得DE⊥AB，AE=BE=
AB=20cm，然后根据勾股定理可计算出AD的长．
解答：∵△ABC折叠，使点B与点A重合，折痕为DE，
∴DE⊥AB，AE=BE=AB=×40cm=20cm，
在Rt△ADE中，DE=15cm，AE=20cm，
∴AD=
=25cm．
故选B．
点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理．
分析：根据折叠的性质得DE⊥AB，AE=BE=
AB=20cm，然后根据勾股定理可计算出AD的长．解答：∵△ABC折叠，使点B与点A重合，折痕为DE，
∴DE⊥AB，AE=BE=
AB=×40cm=20cm，在Rt△ADE中，DE=15cm，AE=20cm，
∴AD=
=25cm．故选B．
点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理．
练习册系列答案
相关题目
如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC边上的中线BD反向延长线交y轴负半轴于E，双曲线
如图，Rt△ABC的两直角边分别为1，2，以Rt△ABC的斜边AC为一直角边，另一直角边为1画第二个△ACD；在以△ACD的斜边AD为一直角边，另一直角边长为1画第三个△ADE；…，依此类推，第n个直角三角形的斜边长是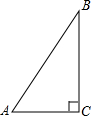
如图，Rt△ABC的斜边AB=10cm，
如图，Rt△ABC的一条直角边AB是⊙O的直径，AB=8，斜边交⊙O于D，∠A=30°，求阴影部分的面积．