题目内容
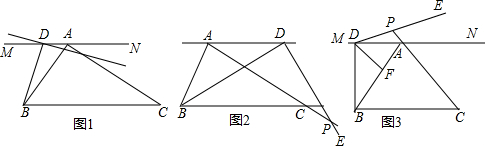
3.探究:(1)如图①,∠1+∠2与∠B+∠C有什么关系?为什么?
当∠A=40°时,∠B+∠C+∠1+∠2=280°.
(2)把图①△ABC沿DE折叠得到△A′DE,如图②,
填空:∠1+∠2=∠B+∠C(填“>”“<”“=”),
如果∠A=30°,则∠A′DB+∠A′EC=60°;猜想∠A′DB、∠A′EC与∠A的关系为∠A′DB+∠A′EC=2∠A,并说明理由.
(3)如图③,把△ABC沿着DE折叠得到△A'DE,则∠A'DB、∠A'EC与∠A的关系为∠A′DB=∠A′EC+2∠A,并说明理由.

分析 (1)根据三角形内角和定理计算即可;
(2)根据翻转变换的性质和三角形内角和定理计算;
(3)根据翻转变换的性质和三角形的外角的性质解答.
解答 解:(1)∠1+∠2=∠B+∠C.
∵∠A+∠1+∠2=180°,∠A+∠B+∠C=180°,
∴∠1+∠2=∠B+∠C,
当∠A=40°时,∠B+∠C=180°-40°=140°,∠1+∠2=180°-40°=140°,
∴∠B+∠C+∠1+∠2=280°,
故答案为:280°;
(2)由(1)得,∠ADE+∠AED=∠B+∠C,
由翻折变换的性质可知,∠1+∠2=∠ADE+∠AED,
∴∠1+∠2=∠B+∠C,
由翻折变换的性质可知,∠ADE=∠A′DE,∠AED=∠A′ED,
∠ADE+∠AED=180°-∠A,
∠ADA′+∠AEA′=360°-2∠A,
∠A′DB+∠A′EC=360°-(360°-2∠A)=2∠A
当∠A=30°时,∠A′DB+∠A′EC=60°,
故答案为:60°;∠A′DB+∠A′EC=2∠A;
(3)∠A'DB=∠A+∠AFD,∠AFD=∠A′+∠A'EC,
∴∠A′DB=∠A′EC+2∠A,
故答案为:∠A′DB=∠A′EC+2∠A.
点评 本题考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
4.已知⊙O的半径为8cm,直线l上有一点B到圆心O的距离等于8cm,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相交或相切 |
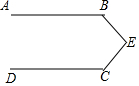 如图,∠B+∠E+∠C=360°,试判断AB与CD是否平行?请说明理由.
如图,∠B+∠E+∠C=360°,试判断AB与CD是否平行?请说明理由.