题目内容
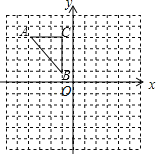
【题目】如图,抛物线
与x轴交于A(3,0)、B(1,0)，与y轴交于点C(0,3)。
(1)求抛物线的解析式；
(2)若点D(0,1)，点P是抛物线上的动点，且△PCD是以CD为底的等腰三角形，求点P的坐标。
【答案】（1）
（2）
【解析】
(1)根据题意可设抛物线的解析式为
，代入点C的坐标就能求解；
(2) △PCD是以CD为底的等腰三角形得出点P是直线y=2与抛物线的交点，把y=2代入解析式求解即可.
解：(1)根据题意可设抛物线的解析式为，
将点C（0,3）代入得
，解得
∴
∴整理可得抛物线的解析式为:
(2)∵△PCD是以CD为底的等腰三角形
∴CD的垂直平分线为y=2
∴点P为直线y=2与抛物线y=-x2+2x+3的交点，
当y=2时，
，解得
，
∴P点坐标为
练习册系列答案
相关题目
【题目】阅读下列内容，并解答问题.
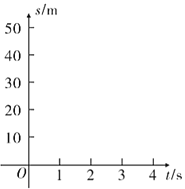
一个滑雪者从山坡滑下，为了得出滑行距离
(单位：
)与滑行时间
(单位：)之间的关系式，测得一些数据(如表)：
滑行时间 | 0 | 1 | 2 | 4 | 5 |
滑行距离 | 0 | 4.5 | 14 | 28.5 | 48 |
为观察与之间的关系，建立坐标系(如图)，以为横坐标，为纵坐标.请解答以下问题：
(1)描出表中数据对应的5个点，并用平滑曲线连接它们；
(2)根据(1)所画出的曲线图象，利用我们所学的函数，近似地表示关于的函数关系式.
