ΧβΡΩΡΎ»ί
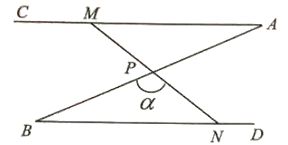
ΓΨΧβΡΩΓΩΈ“Ο«≤ΜΖΝ‘ΦΕ®ΘΚ‘Ύ÷±Ϋ«ΓςABC÷–Θ§»γΙϊΫœ≥ΛΒΡ÷±Ϋ«±ΏΒΡ≥ΛΕ»ΈΣΫœΕΧ÷±Ϋ«±Ώ≥ΛΕ»ΒΡΝΫ±ΕΘ§‘ρ≥Τ÷±Ϋ«ΓςABCΈΣΜΤΫπ»ΐΫ«–Έ
Θ®1Θ©“―÷ΣΘΚΒψOΘ®0Θ§0Θ©Θ§ΒψAΘ®2Θ§0Θ©Θ§œ¬Ν–y÷α’ΐΑκ÷α…œΒΡΒψΡή”κΒψOΘ§ΒψAΙΙ≥…ΜΤΫπ»ΐΫ«–ΈΒΡ”–ΓΓΓΓΘΜΧν–ρΚ≈ΔΌΘ®0Θ§1Θ©ΘΜΔΎΘ®0Θ§2Θ©ΘΜΔέΘ®0Θ§3Θ©Θ§ΔήΘ®0Θ§4Θ©ΘΜ
Θ®2Θ©“―÷ΣΒψPΘ®5Θ§0Θ©Θ§≈–Εœ÷±œΏy=2x-6‘ΎΒΎ“Μœσœό «Ζώ¥φ‘ΎΒψQΘ§ ΙΒΟΓςOPQ «ΜΤΫπ»ΐΫ«–ΈΘ§»τ¥φ‘Ύ«σ≥ωΒψQΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…ΘΜ
Θ®3Θ©“―÷ΣΘΚΖ¥±»άΐΚ· ΐ![]() ”κ÷±œΏy=-x+m+1ΫΜ”ΎMΘ§NΝΫΒψΘ§»τ‘Ύx÷α…œ”–«“÷Μ”–“ΜΗωΒψCΘ§ ΙΒΟΓœMCN=90
”κ÷±œΏy=-x+m+1ΫΜ”ΎMΘ§NΝΫΒψΘ§»τ‘Ύx÷α…œ”–«“÷Μ”–“ΜΗωΒψCΘ§ ΙΒΟΓœMCN=90![]() Θ§«σmΒΡ÷ΒΘ§≤Δ≈–Εœ¥Υ ±ΓςMNC «ΖώΈΣΜΤΫπ»ΐΫ«–ΈΘ°
Θ§«σmΒΡ÷ΒΘ§≤Δ≈–Εœ¥Υ ±ΓςMNC «ΖώΈΣΜΤΫπ»ΐΫ«–ΈΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌΔήΘΜΘ®2Θ©QΉχ±ξΈΣΘ®5Θ§4Θ©ΘΜΘ®3Θ© «ΜΤΫπ»ΐΫ«–Έ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΜΤΫπ»ΐΫ«–ΈΒΡΕ®“εΦ¥Ω…≈–ΕœΘ°
Θ®2Θ©ΦΌ…η¥φ‘ΎΘ°…ηQ(m,2m6)Θ§Ζ÷ΝΫ÷÷«ι–ΈΖ÷±π«σΫβΦ¥Ω…Θ°
Θ®3Θ©…ηM(x1,y1)Θ§N(x2,y2)Θ§MNΒΡ÷–ΒψΈΣkΘ§Β±ΒψKΒΫx÷αΒΡΨύάκΒ»”Ύ![]() ±Θ§¬ζΉψΧθΦΰΘ°ΗυΨί“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐΒΡΙΊœΒΘ§ΙΙΫ®ΖΫ≥Χ«σ≥ωmΦ¥Ω…≈–ΕœΘ°
±Θ§¬ζΉψΧθΦΰΘ°ΗυΨί“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐΒΡΙΊœΒΘ§ΙΙΫ®ΖΫ≥Χ«σ≥ωmΦ¥Ω…≈–ΕœΘ°
ΫβΘΚΘ®1Θ©“ρΈΣΒψ![]() Θ®0Θ§0Θ©Θ§Βψ
Θ®0Θ§0Θ©Θ§Βψ![]() Θ®2Θ§0Θ©Θ§ΗυΨίΜΤΫπ»ΐΫ«–ΈΒΡΕ®“εΩ…÷Σ‘Ύy÷α’ΐΑκ÷α…œΒΡΒψ
Θ®2Θ§0Θ©Θ§ΗυΨίΜΤΫπ»ΐΫ«–ΈΒΡΕ®“εΩ…÷Σ‘Ύy÷α’ΐΑκ÷α…œΒΡΒψ
”κ‘≠ΒψΒΡœΏΕΈ≥ΛΕ»ΈΣ1Μρ’Ώ4Θ§Ι ΫαΚœΧβΡΩΩ…÷Σ”κΒψ![]() Θ§Βψ
Θ§Βψ![]() ΙΙ≥…ΜΤΫπ»ΐΫ«–ΈΒΡ”–
ΙΙ≥…ΜΤΫπ»ΐΫ«–ΈΒΡ”–![]() Μρ
Μρ![]() Θ§Ι ¥πΑΗΈΣΔΌΔήΘ°
Θ§Ι ¥πΑΗΈΣΔΌΔήΘ°
Θ®2Θ©ΦΌ…η¥φ‘ΎΘ°…η![]() Θ§
Θ§
![]() «÷±Ϋ«»ΐΫ«–ΈΘ§Β±
«÷±Ϋ«»ΐΫ«–ΈΘ§Β±![]() «÷±Ϋ«»ΐΫ«–Έ ±Θ§
«÷±Ϋ«»ΐΫ«–Έ ±Θ§![]() Θ§
Θ§
![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() ΚΆ4Θ§
ΚΆ4Θ§
![]() Βψ
Βψ![]() ‘ΎΒΎ“ΜœσœόΘ§
‘ΎΒΎ“ΜœσœόΘ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «ΜΤΫπ»ΐΫ«–ΈΘ§
«ΜΤΫπ»ΐΫ«–ΈΘ§
Β±![]() ±Θ§
±Θ§![]() Θ§¥Υ ±
Θ§¥Υ ±![]() ≤Μ¬ζΉψΜΤΫπ»ΐΫ«–ΈΒΡΕ®“εΘ°
≤Μ¬ζΉψΜΤΫπ»ΐΫ«–ΈΒΡΕ®“εΘ°
![]() ¬ζΉψΧθΦΰΒψΒψ
¬ζΉψΧθΦΰΒψΒψ![]() Ήχ±ξΈΣ
Ήχ±ξΈΣ![]() Θ°
Θ°
Θ®3Θ©…η![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡ÷–ΒψΈΣ
ΒΡ÷–ΒψΈΣ![]() Θ§Β±Βψ
Θ§Β±Βψ![]() ΒΫ
ΒΫ![]() ÷αΒΡΨύάκΒ»”Ύ
÷αΒΡΨύάκΒ»”Ύ![]() ±Θ§¬ζΉψΧθΦΰΘ°
±Θ§¬ζΉψΧθΦΰΘ°
”…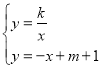 Θ§œϊ»Ξ
Θ§œϊ»Ξ![]() ΒΟΒΫΘΚ
ΒΟΒΫΘΚ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°![]() Θ§
Θ§
![]()
![]() Θ§
Θ§![]() Θ§
Θ§![]()
![]() Θ§
Θ§
’ϊάμΒΟΘΚ![]() Θ§
Θ§![]() Θ§
Θ§
»γΆΦΘ§Ής![]() ÷α”Ύ
÷α”Ύ![]() Θ°
Θ°
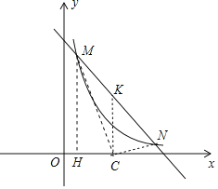
![]() ÷±œΏ
÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() ≤Μ «ΜΤΫπ»ΐΫ«–ΈΘ°
≤Μ «ΜΤΫπ»ΐΫ«–ΈΘ°

 ΫΉΧίΦΤΥψœΒΝ–¥πΑΗ
ΫΉΧίΦΤΥψœΒΝ–¥πΑΗ