题目内容
在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
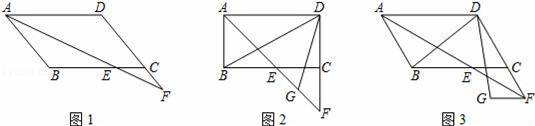
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.

【考点】平行四边形的判定与性质;全等三角形的判定与性质;等边三角形的判定与性质;菱形的判定与性质.
【专题】几何综合题;压轴题.
【分析】(1)根据AF平分∠BAD,可得∠BAF=∠DAF,利用四边形ABCD是平行四边形,求证∠CEF=∠F即可.
(2)根据∠ABC=90°,G是EF的中点可直接求得.
(3)分别连接GB、GC,求证四边形CEGF是平行四边形,再求证△ECG是等边三角形.
由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB,求证△BEG≌△DCG,然后即可求得答案
【解答】(1)证明:如图1,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠F,
∴∠CEF=∠F.
∴CE=CF.
(2)解:连接GC、BG,
∵四边形ABCD为平行四边形,∠ABC=90°,
∴四边形ABCD为矩形,
∵AF平分∠BAD,
∴∠DAF=∠BAF=45°,
∵∠DCB=90°,DF∥AB,
∴∠DFA=45°,∠ECF=90°
∴△ECF为等腰直角三角形,
∵G为EF中点,
∴EG=CG=FG,CG⊥EF,
∵△ABE为等腰直角三角形,AB=DC,
∴BE=DC,
∵∠CEF=∠GCF=45°,
∴∠BEG=∠DCG=135°
在△BEG与△DCG中,
∵
 ,
,
∴△BEG≌△DCG,
∴BG=DG,
∵CG⊥EF,
∴∠DGC+∠DGA=90°,
又∵∠DGC=∠BGA,
∴∠BGA+∠DGA=90°,
∴△DGB为等腰直角三角形,
∴∠BDG=45°.
(3)解:延长AB、FG交于H,连接HD.
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形
∵∠ABC=120°,AF平分∠BAD
∴∠DAF=30°,∠ADC=120°,∠DFA=30°
∴△DAF为等腰三角形
∴AD=DF,
∴CE=CF,
∴平行四边形AHFD为菱形
∴△ADH,△DHF为全等的等边三角形
∴DH=DF,∠BHD=∠GFD=60°
∵FG=CE,CE=CF,CF=BH,
∴BH=GF
在△BHD与△GFD中,
∵
 ,
,
∴△BHD≌△GFD,
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°






【点评】此题主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.同学们在解决此类问题时,可以通过以下的步骤进行思考和分析:(1)通过测量或特殊情况的提示进行猜想;(2)根据猜想的结果进行联想(如60度角可以联想到等边三角形,45度角可以联想到等腰直角三角形等);(3)在联想的基础上根据已知条件利用几何变换(如旋转、平移、轴对称等)构造全等解决问题.

 阅读快车系列答案
阅读快车系列答案
 .
.

 D.
D.

 )﹣1﹣2cos30°+
)﹣1﹣2cos30°+
 +(2﹣π)0
+(2﹣π)0 D.x2+2x=x2﹣1
D.x2+2x=x2﹣1