题目内容

精英家教网如图，点A是函数y=
4
x
(x＞0)图象上的一个动点，点B为线段OA的中点，则过点A的⊙B的面积不可能是（　　）
A、4πB、3πC、2πD、π
分析：根据题意，OA为圆的直径，要求圆的面积的范围，即求OA的范围，由反比例函数的性质可知，OA只有最小值，没有最大值，即转化为求OA的最小值，由反比例函数性质知，当OA为∠yox的角平分线时OA最小，求得最小面积为2π，所以D不可能．
解答：解：∵点B为线段OA的中点，
∴OA为圆的直径，
由题意知为求面积范围，即要确定OA的范围，
又根据反比例函数图象性质，OA只有最小值，且当OA为yox的角平分线时OA最小，
此时A点的坐标为（2，2），
∴OA=2
2
，
∴Smin=2π，
∴面积不可能是π，
故选D．
点评：本题考查反比例函数图象性质，及其点坐标特征，要善于转换思维，发现题的切入点．
练习册系列答案
相关题目
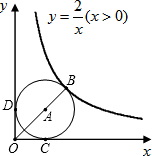精英家教网如图，点A是函数y=
1
x
的图象上的点，点B、C的坐标分别为B（-
2
，-
2
）、C（
2
，
2
），试利用性质：“函数y=
1
x
的图象上任意一点A都满足|AB-AC|=2
2
”求解下面问题：作∠BAC的内角平分线AE，过B作AE的垂线交AE于F，已知当点A在函数y=
1
x
的图象上运动时，点F总在一个圆上运动，则这圆的半径为（　　）
A、1
B、
2
2
C、
2
D、
3
2
2
精英家教网如图，点B是函数y=
2x
(x＞0)图象上一点，点A是线段OB上一点，以AB为半径作⊙A恰好与x轴、y轴分别切于点C和点D，则点A的坐标是
 
．
精英家教网如图，点M是函数y=x+
1x
图象上的一点，直线l：y=x，过点M分别作MA⊥y轴，MB⊥l，A，B为垂足，则MA•MB=
 
．
如图①，抛物线y=
1
2
x2+x-4与x轴的两个交点分别为A、B，与y轴的交点为C．
（1）请直接写出点A、B、C的坐标；
（2）如图①，点Q是函数y=
1
2
x2+x-4的图象在第三象限上的任一点，点Q的横坐标为m，设四边形AQCB的面积为S，求S与m之间的函数关系式，并求出m这何值时，S有最大值，最大值是多少？
（3）抛物线y=
1
2
x2+x-4的对称轴上是否存在一点H，使△BCH的周长最小？若存在，请直接写出H点坐标；若不存在，请说明理由．
（4）如图②，若点E为线段BC的中点，EF垂直平分BC交x轴于点F（-3，0），点P是抛物线y=
1
2
x2+x-4对称轴上的一点，设P点的纵坐标为t，请直接写出∠PEC为钝角三角形时t的取值范围．
精英家教网如图，点B是函数y=
1
x
和y=x的图象在第一象限的交点，点E在函数y=
1
x
的图象上，过B、E两点作x轴的垂线，垂足分别为C、F，直线EF与直线y=x交于点D．试判断DF+EF与2BC的大小，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网