题目内容
2.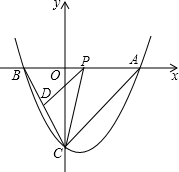 如图,抛物线y=$\frac{1}{2}{x^2}$-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
如图,抛物线y=$\frac{1}{2}{x^2}$-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.(1)直接写出A、B、C的坐标;
(2)求抛物线y=$\frac{1}{2}{x^2}$-x-4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
分析 (1)设y=0,解一元二次方程即可求出A和B的坐标,设x=0,则可求出C的坐标.
(2)抛物线:$y=\frac{1}{2}{x}^{2}-x-4=\frac{1}{2}(x-1)^{2}-\frac{9}{2}$,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-$\frac{9}{2}$).
(3)设P(x,0)(-2<x<4),由PD∥AC,可得到关于PD的比例式,由此得到PD和x的关系,再求出C到PD的距离(即P到AC的距离),利用三角形的面积公式可得到S和x的函数关系,利用函数的性质即可求出三角形面积的最大值,进而得到x的值,所以PD可求,而PA≠PD,所以PA、PD为邻边的平行四边形不是菱形.
解答 解:(1)A(4,0)、B(-2,0)、C(0,-4).
(2)抛物线:$y=\frac{1}{2}{x}^{2}-x-4=\frac{1}{2}(x-1)^{2}-\frac{9}{2}$,
∴抛物线的对称轴是直线x=1,顶点坐标是(1,-$\frac{9}{2}$).
(3)设P(x,0)(-2<x<4),
∵PD∥AC,
∴$\frac{PD}{AC}=\frac{BP}{AB}$,
解得:$PD=\frac{{2\sqrt{2}}}{3}(x+2)$,
∵C到PD的距离(即P到AC的距离):$d=PA×sin{45^0}=\frac{{\sqrt{2}}}{2}(4-x)$,
∴△PCD的面积$S=\frac{1}{2}×PD×d=\frac{1}{3}(x+2)(4-x)=-\frac{1}{3}{x^2}+\frac{2}{3}x+\frac{8}{3}$,
∴$S=-\frac{1}{3}{(x-1)^2}+3$,
∴△PCD面积的最大值为3,
当△PCD的面积取最大值时,x=1,PA=4-x=3,$PD=\frac{{2\sqrt{2}}}{3}(x+2)=2\sqrt{2}$,
因为PA≠PD,所以以PA、PD为邻边的平行四边形不是菱形.
点评 本题考查了二次函数和坐标轴的交点问题、平行线分线段成比例定理、特殊角的锐角三角形函数值、二次函数的最值问题以及菱形的判定,题目的综合性较强,难度中等.

 53天天练系列答案
53天天练系列答案| A. | ±81 | B. | 81 | C. | ±3 | D. | 3 |
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
| A. | y=x-2 | B. | $y=\frac{1}{x-2}$ | C. | $y=\sqrt{x-2}$ | D. | $y=\frac{1}{{\sqrt{x-2}}}$ |
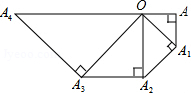 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OAn的长度为$\sqrt{{2}^{n}}$.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OAn的长度为$\sqrt{{2}^{n}}$.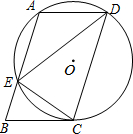 如图,在?ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
如图,在?ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.