题目内容
10. 如图,D、E分别是△ABC的边AB、AC上的点,∠1=∠B,AE=EC=4,BC=10,AB=12,则△ADE和△ACB的周长之比为( )
如图,D、E分别是△ABC的边AB、AC上的点,∠1=∠B,AE=EC=4,BC=10,AB=12,则△ADE和△ACB的周长之比为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 由于∠1=∠B,且∠A是公共角,可以得到△ADE∽△ACB;AE与AB是对应边,因而相似比是4:12=1:3,相似三角形的周长的比等于相似比,即1:3.
解答 解:∵∠1=∠B,∠A=∠A,
∴△ADE∽△ACB,
∴C△ADE:C△ABC=AE:AB=1:3.
故选B.
点评 本题考查了相似三角形性质和判定,相似三角形的周长比等于相似比.解决本题的关键是弄清相似三角形的对应边.

练习册系列答案
相关题目
1.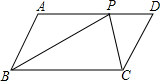 如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )
如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )
 如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )
如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )| A. | S1+S3<S2 | B. | S1+S3>S2 | C. | S1+S3=S2 | D. | S1+S2=S3 |
2. 将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
 将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )| A. |  | B. |  | C. |  | D. |  |
19.若|x+y-1|+(y+3)2=0,则$\frac{1}{4}$x-2y的值是( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
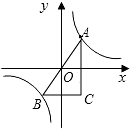 如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积.
如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积.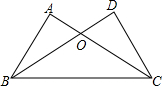 如图,AC、BD相交于点O,∠A=∠D,请你根据(SAS)全等三角形的判定再补充一个条件,使得△ABC≌△DCB,你补充的条件是OB=OC.
如图,AC、BD相交于点O,∠A=∠D,请你根据(SAS)全等三角形的判定再补充一个条件,使得△ABC≌△DCB,你补充的条件是OB=OC. 如图,矩形ABCD中,AB=6,BC=10.请你设计一种方案,把此矩形剪成两块,并拼成一个菱形(要求在原图上画出分割线,并画出拼后的菱形,标上字母和能反映剪拼方法的数据).
如图,矩形ABCD中,AB=6,BC=10.请你设计一种方案,把此矩形剪成两块,并拼成一个菱形(要求在原图上画出分割线,并画出拼后的菱形,标上字母和能反映剪拼方法的数据).