题目内容
13. 如图,正方形AEDC的面积为25cm2,测量出AB=12cm,BC=13cm,E,A,B三点在一条直线上吗?为什么?
如图,正方形AEDC的面积为25cm2,测量出AB=12cm,BC=13cm,E,A,B三点在一条直线上吗?为什么?
分析 先由正方形AEDC的面积为25cm2,可求AC的长为5cm,然后由勾股定理的逆定理可证△ABC是直角三角形,且∠CAB=90°,进而可得∠EAB=180°,即可证E,A,B三点在一条直线上.
解答 解:E,A,B三点在一条直线上.
理由:∵正方形AEDC的面积为25cm2,
∴∠EAC=90°,AC=5cm,
在△ABC中,
∵AC2+AB2=25+144=169=132=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴∠EAC+∠BAC=180°=∠EAB,
即E,A,B三点在一条直线上.
点评 此题考查了正方形的性质、勾股定理的逆定理及三点共线,解题的关键是:理解证明E,A,B三点在一条直线上,即证∠EAB=180°.

练习册系列答案
相关题目
4.下列结论中,正确的是( )
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若a>b,则a2>b2 | C. | 若a>b,则1-a<1-b | D. | 若a>b,ac2>bc2 |
8.下列运算中,正确的是( )
| A. | x2+x3=x5 | B. | (x2)3=x6 | C. | 2x3÷x2=x | D. | 2x-1=$\frac{1}{2x}$ |
18. 与左边左视图所对应的实物图是( )
与左边左视图所对应的实物图是( )
 与左边左视图所对应的实物图是( )
与左边左视图所对应的实物图是( )| A. |  | B. |  | C. |  | D. |  |
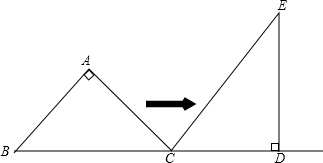 等腰直角三角形△ABC的斜边BC与直角△CDE的直角边CD在同一直线上,∠A=∠EDC=90°,BC=DE=4,CE=5,将△ABC沿着BD向右平移,当点A落在CE上时,平移距离为$\frac{7}{2}$.
等腰直角三角形△ABC的斜边BC与直角△CDE的直角边CD在同一直线上,∠A=∠EDC=90°,BC=DE=4,CE=5,将△ABC沿着BD向右平移,当点A落在CE上时,平移距离为$\frac{7}{2}$.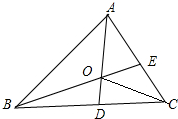 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断: