题目内容
11.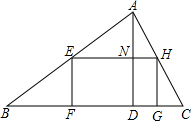 如图,在锐角三角形ABC中,边BC=120cm,高AD=80cm,矩形EFGH的顶点E、H分别在AB、AC上,F、G在BC上,AD与EH交于点N.
如图,在锐角三角形ABC中,边BC=120cm,高AD=80cm,矩形EFGH的顶点E、H分别在AB、AC上,F、G在BC上,AD与EH交于点N.(1)试说明:△AEH∽△ABC;
(2)若矩形EFGH是正方形,求EH的长;
(3)当EH为何值时,矩形EFGH的面积最大?最大值是多少?
分析 (1)根据EF∥FG,可得△AEH∽△ABC;
(2)根据相似三角形的性质:相似三角形的对应高之比等于相似比,列式计算可得答案;
(3)根据矩形的面积计算公式,可得二次函数,根据二次函数的性质,可得矩形EFGH的面积最大值.
解答  解:(1)在矩形EFGH中,EF∥FG,
解:(1)在矩形EFGH中,EF∥FG,
∴△AEH∽△ABC;
(2)设EH=xcm,
由△AEH∽△ABC得$\frac{EH}{BC}$=$\frac{AN}{AD}$,
即$\frac{x}{120}$=$\frac{80-EF}{80}$,
∴EF=80-$\frac{2}{3}$x,
∵矩形EFGH是正方形,
∴EF=EH,
∴x=80-$\frac{2}{3}$x,
解得x=48,
即EH=48cm.
(3)S矩形EFGH=EF•EH=x(80-$\frac{2}{3}$x)=-$\frac{2}{3}$(x-60)2+2400,
即当EH=60cm时,矩形EFGH的面积的最大值是2400cm2.
点评 本题考查了相似三角形的判定与性质,二次函数的最值以及矩形、正方形的性质的运用,解题时注意:相似三角形的对应高之比等于相似比.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
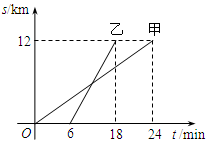 甲、乙两人以相同路线前往离学校12km的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,求每分钟乙比甲多行驶多少千米.
甲、乙两人以相同路线前往离学校12km的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,求每分钟乙比甲多行驶多少千米. 如图,正方形ABCD的边长为6$\sqrt{2}$,点E是边CD的中点,点F在边BC上,AE、AF分别与对角线BD交于点G、H,点M、N分别是线段GH、EF的中点,若∠EAF=45°,则线段MN的长为$\frac{5}{2}$.
如图,正方形ABCD的边长为6$\sqrt{2}$,点E是边CD的中点,点F在边BC上,AE、AF分别与对角线BD交于点G、H,点M、N分别是线段GH、EF的中点,若∠EAF=45°,则线段MN的长为$\frac{5}{2}$.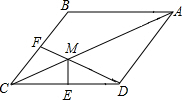 如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠BAC=∠CDF.
如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠BAC=∠CDF.