题目内容
4.在等腰三角形中,AC=BC=20,AB=24,点E,F分别是线段AB,AC上的动点,(点E不与A,B重合)且∠CEF=∠B,则当AE=20或$\frac{50}{3}$时,△EFC为等腰三角形.分析 分类讨论:当EC=EF,如图1,证明△AEC为等腰三角形,得到AE=AC=20;当FC=FE,如图2,证明△EAC∽△CAB,利用相似比计算AE的长.
解答 解:当EC=EF,如图1,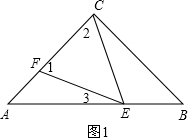
∴∠1=∠2,
∵AB=AC=20,
∴∠A=∠B,
∵∠CEF=∠B,
∴∠A=∠CEF,
∵∠1=∠A+∠3,
∴∠1=∠CEF+∠3=∠AEC,
∴∠AEC=∠2,
∴AE=AC=20;
当FC=FE,如图2,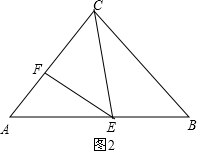
∴∠ECF=∠CEF,
∵∠CEF=∠B=∠A,
∴∠A=∠B=∠ACE,
∴△EAC∽△CAB,
∴$\frac{AE}{CA}$=$\frac{CA}{AB}$,即$\frac{AE}{20}$=$\frac{20}{24}$,
∴AE=$\frac{50}{3}$,
综上所述,AE的长为20或$\frac{50}{3}$.
故答案为20或$\frac{50}{3}$.
点评 本题考查了相似三角形的判定与性质:判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了等腰三角形的判定与性质和分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.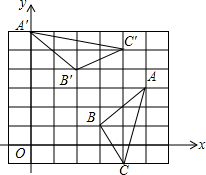 如图,将△ABC绕点P逆时针旋转90°得到△A′B′C,则点P的坐标是( )
如图,将△ABC绕点P逆时针旋转90°得到△A′B′C,则点P的坐标是( )
 如图,将△ABC绕点P逆时针旋转90°得到△A′B′C,则点P的坐标是( )
如图,将△ABC绕点P逆时针旋转90°得到△A′B′C,则点P的坐标是( )| A. | (1,1) | B. | (2,1) | C. | (1,2) | D. | (1,3) |
16.闽侯县历史悠久,地处福建省东部,福州市西南侧,总面积约2140平方公里,呈月芽形拱卫省会城市,是福建最靠近省会城市的一个县.历史悠久,素称“八闽首邑“.将2140用科学记数法表示为( )
| A. | 2.14×103 | B. | 2.14×104 | C. | 21.4×102 | D. | 0.214×104 |
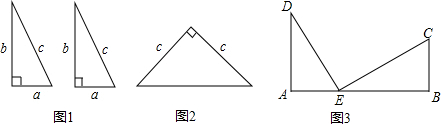
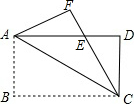 如图,将矩形ABCD沿对角线AC折叠,B点落在F,FC与AD交于E点,求证:ED=EF.
如图,将矩形ABCD沿对角线AC折叠,B点落在F,FC与AD交于E点,求证:ED=EF.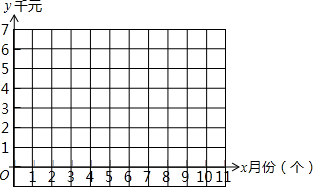 在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;
在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;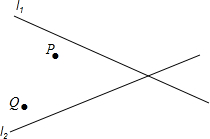 如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).
如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).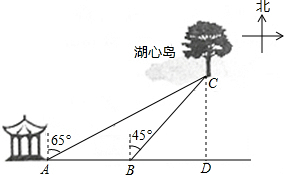 如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).
如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).