题目内容
如图,Rt△ABC的两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动,速度是1cm/秒,同时,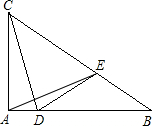 点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.
点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.(1)当动点运动几秒时,△BDE与△ABC相似?
(2)设动点运动t秒时△ADE的面积为s,求s与t的函数解析式;
(3)在运动过程中是否存在某一时刻t,使CD⊥DE?若存在,求出时刻t;若不存在,请说明理由.
分析:设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤
),
(1)分类:当∠BDE=∠BAC,即ED⊥AB时,Rt△BDE∽Rt△BAC;当∠BDE=∠BAC,即DE⊥AB时,Rt△BDE∽Rt△BCA,然后分别根据三角形相似的性质得到比例线段求出t的值;
(2)过E作EF⊥AB于F,易证Rt△BEF∽Rt△BAC,根据三角形相似的性质得到比例线段用t表示EF,BF,然后根据三角形的面积公式求解即可;
(3)先计算出DF=AB-AD-BF,若CD⊥DE,则易证得Rt△ACD∽Rt△FDE,然后根据三角形相似的性质得到比例线段求出t.
| 5 |
| 2 |
(1)分类:当∠BDE=∠BAC,即ED⊥AB时,Rt△BDE∽Rt△BAC;当∠BDE=∠BAC,即DE⊥AB时,Rt△BDE∽Rt△BCA,然后分别根据三角形相似的性质得到比例线段求出t的值;
(2)过E作EF⊥AB于F,易证Rt△BEF∽Rt△BAC,根据三角形相似的性质得到比例线段用t表示EF,BF,然后根据三角形的面积公式求解即可;
(3)先计算出DF=AB-AD-BF,若CD⊥DE,则易证得Rt△ACD∽Rt△FDE,然后根据三角形相似的性质得到比例线段求出t.
解答: 解:设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤
解:设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤
),
(1)当∠BDE=∠BAC,即ED⊥AB时,Rt△BDE∽Rt△BAC,
∴BD:BA=BE:BC,即(4-t):4=2t:5,
∴t=
;
当∠BDE=∠BAC,即DE⊥AB时,Rt△BDE∽Rt△BCA,
∴BD:BC=BE:BA,即(4-t):5=2t:4,
∴t=
;
所以当动点运动
秒或
秒时,△BDE与△ABC相似;
(2)过E作EF⊥AB于F,如图,
易证Rt△BEF∽Rt△BAC,
∴EF:AC=BF:AB=BE:BC,即EF:3=BF:4=2t:5,
∴EF=
,BF=
,
∴S=
AD•EF=
•t•
=
t2(0≤t≤
);
(3)存在.
DF=AB-AD-BF=4-t-
=4-
t,
若CD⊥DE,
易证得Rt△ACD∽Rt△FDE,
∴AC:DF=AD:EF,即3:(4-
t)=t:
,
∴t=
.
 解:设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤
解:设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤| 5 |
| 2 |
(1)当∠BDE=∠BAC,即ED⊥AB时,Rt△BDE∽Rt△BAC,
∴BD:BA=BE:BC,即(4-t):4=2t:5,
∴t=
| 20 |
| 13 |
当∠BDE=∠BAC,即DE⊥AB时,Rt△BDE∽Rt△BCA,
∴BD:BC=BE:BA,即(4-t):5=2t:4,
∴t=
| 8 |
| 7 |
所以当动点运动
| 20 |
| 13 |
| 8 |
| 7 |
(2)过E作EF⊥AB于F,如图,
易证Rt△BEF∽Rt△BAC,
∴EF:AC=BF:AB=BE:BC,即EF:3=BF:4=2t:5,
∴EF=
| 6t |
| 5 |
| 8t |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 6t |
| 5 |
| 3 |
| 5 |
| 5 |
| 2 |
(3)存在.
DF=AB-AD-BF=4-t-
| 8t |
| 5 |
| 13 |
| 5 |
若CD⊥DE,
易证得Rt△ACD∽Rt△FDE,
∴AC:DF=AD:EF,即3:(4-
| 13 |
| 5 |
| 6t |
| 5 |
∴t=
| 2 |
| 13 |
点评:本题考查了三角形相似的判定与性质:两组角对应相等的两三角形相似;相似三角形的对应边的比相等.也考查了勾股定理以及分类讨论思想的运用.

练习册系列答案
相关题目
 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线 如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是
如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是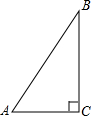 如图,Rt△ABC的斜边AB=10cm,
如图,Rt△ABC的斜边AB=10cm,
 如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.
如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.