题目内容
已知x为实数,则 的最大值是________.
的最大值是________.
2
分析:设y= +
+ ,然后把等式两边平方,再根据二次函数的最值问题求出y2的最大值,开方即可得解.
,然后把等式两边平方,再根据二次函数的最值问题求出y2的最大值,开方即可得解.
解答:设y= +
+ ,
,
则y2=8-x+2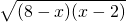 +x-2=2
+x-2=2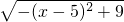 +6,
+6,
∴当x=5时,y2有最大值,为12,
∴y的最大值是 =2
=2 ,
,
即 +
+ 的最大值是2
的最大值是2 .
.
故答案为:2 .
.
点评:本题考查了二次函数的最值问题,利用二次函数的最值问题求出所求代数式的平方的最大值是解题的关键.

分析:设y=
 +
+ ,然后把等式两边平方,再根据二次函数的最值问题求出y2的最大值,开方即可得解.
,然后把等式两边平方,再根据二次函数的最值问题求出y2的最大值,开方即可得解.解答:设y=
 +
+ ,
,则y2=8-x+2
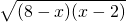 +x-2=2
+x-2=2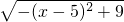 +6,
+6,∴当x=5时,y2有最大值,为12,
∴y的最大值是
 =2
=2 ,
,即
 +
+ 的最大值是2
的最大值是2 .
.故答案为:2
 .
.点评:本题考查了二次函数的最值问题,利用二次函数的最值问题求出所求代数式的平方的最大值是解题的关键.

练习册系列答案
相关题目
已知a为实数,则代数式
的最小值为( )
| 27-12a+2a2 |
| A、0 | ||
| B、3 | ||
C、3
| ||
| D、9 |
已知a为实数,则代数式
的最小值为( )
| 2a2-12a+27 |
| A、0 | ||
| B、3 | ||
C、3
| ||
| D、9 |
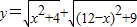 的最小值.要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于
的最小值.要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于 的线段,再比较
的线段,再比较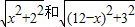 和矩形对角线的大小.
和矩形对角线的大小.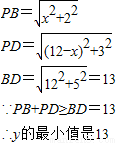
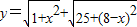 的最小值.
的最小值.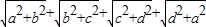 的最小值.
的最小值.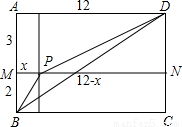
 的最小值为( )
的最小值为( )