Question

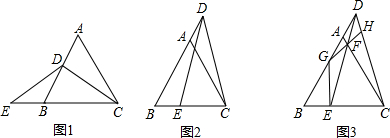
9．为了测得如图（1）和图（2）中的两棵树的高度，在同一时刻小颖分别做了如下操作：图（1）中：测得竹竿CD的长为1米，其影子长CE为1.2米，以及图（1）中树AB的影子AE的长为4.8米．
图（2）中：测得落在地面上树的影子长BC为3.2米，落在墙上的影子的高CD为1米．根据小颖提供的这些条件你能分别求出图（1）和图（2）中的树的高度吗？试试看．

Answer 1

分析 （1）根据在同一时刻物高与影长的比相等，可得$\frac{AB}{4.8}$=$\frac{1}{1.2}$，解此比例式即可得出答案；
（2）先求出墙上的影高落在地面上时的长度，再设树高为h，根据同一时刻物高与影长成正比列出关系式求出h的值即可．

解答 解：（1）根据题意，得$\frac{AB}{4.8}$=$\frac{1}{1.2}$，
解得AB=4．
即图（1）中的树高为4米；

（2）设墙上的影高落在地面上时的长度为x，树高为h，
∵竹竿CD的长为1米，其影子长CE为1.2米，
∴$\frac{1}{1.2}$=$\frac{1}{x}$，解得x=1.2，
∴树的影长为：3.2+1.2=4.4（米），
∴$\frac{h}{4.4}$=$\frac{1}{1.2}$，
解得h=$\frac{11}{3}$．
即图（2）中的树高为$\frac{11}{3}$米．

点评 本题考查的是相似三角形的应用，解答此题的关键是正确求出树的影长，这是此题的易错点．