题目内容
8.下列命题:①两直线平行,同旁内角互补; ②三角形的外角和是180°; ③面积相等的三角形是全等三角形;④若n<1,则n2-1<0;其中,假命题的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别利用平行线的性质、三角形的外角和定理、全等三角形的判定方法等知识分别判断后即可确定正确的选项.
解答 解:①两直线平行,同旁内角互补,正确,为真命题;
②三角形的外角和是360°,故错误,为假命题;
③面积相等的三角形是全等三角形,错误,为假命题;
④若n<1,则n2-1<0当n=-3时,错误,故为假命题,
假命题有3个,
故选C.
点评 本题考查了命题与定理的知识,解题的关键是了解平行线的性质、三角形的外角和定理、全等三角形的判定方法等知识,难度不大.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
19.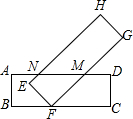 张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )
张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )
 张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )
张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
16.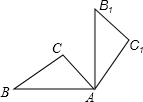 在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )
在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )
 在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )
在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )| A. | 5$\sqrt{2}$ | B. | $\frac{25}{4}$πcm2 | C. | $\frac{25}{2}$πcm2 | D. | 5πcm2 |
3.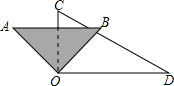 如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
 如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )| A. | ∠AOD>∠BOC | B. | ∠AOC≠∠BOD | C. | ∠AOD-∠BOC=45° | D. | ∠AOD+∠BOC=180° |
20.如果关于x的不等式组$\left\{\begin{array}{l}{x>2}\\{x>m}\end{array}\right.$的解集是x>2,那么m的取值范围是( )
| A. | m≤2 | B. | m≥2 | C. | m≤1 | D. | m>1 |
18.正n边形的每一个外角都不大于40°,则满足条件的多边形边数最少为( )
| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
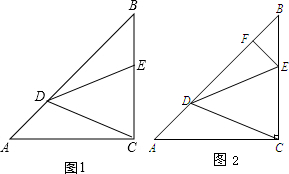 △ABC中,AC=BC,∠ACB=90°,点D,E分别在AB,BC上,且AD=BE,BD=AC.
△ABC中,AC=BC,∠ACB=90°,点D,E分别在AB,BC上,且AD=BE,BD=AC. 如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )