题目内容
如图，△ABC内接于⊙O，点D为⊙O上的一点，DE∥CB交AB延长线于点E．求证：AC•BE=BD•CD．考点：圆周角定理,相似三角形的判定与性质
专题：证明题
分析：首先连接AD，由DE∥BC，可得∠EBD=∠CBD，∠ABC=∠E，由圆周角定理可得∠CBD=∠CAD，∠ABC∠ADC，继而证得△EBD∽△DCA，然后由相似三角形的对应边成比例，证得结论．
解答：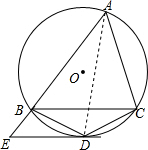
证明：连接AD，
∵DE∥BC，
∴∠EBD=∠CBD，∠ABC=∠E，
∵∠CBD=∠CAD，∠ABC∠ADC，
∴∠EDB=∠CAD，∠ADC=∠E，
∴△EBD∽△DCA，
∴BE：CD=BD：AC，
∴AC•BE=BD•CD．
证明：连接AD，∵DE∥BC，
∴∠EBD=∠CBD，∠ABC=∠E，
∵∠CBD=∠CAD，∠ABC∠ADC，
∴∠EDB=∠CAD，∠ADC=∠E，
∴△EBD∽△DCA，
∴BE：CD=BD：AC，
∴AC•BE=BD•CD．
点评：此题考查了圆周角定理以及相似三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
若函数y=kx+b图象如图所示，则关于x的不等式kx+b＜0的解集为
把四张形状大小完成相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为m厘米，宽为n厘米）的盒子底部（如图②）盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的两个小长方形的周长和是