Question

【题目】如图1，抛物线与x轴交于A、B两点，与y轴交于点C.直线经过抛物线与坐标轴的两个交点B和C。

（1）求直线BC的解析式；

（2）点D是线段BC上的一个动点（与两个端点均不重合），过点D引y轴的平行线PD交抛物线于点P，设抛物线的对称轴为直线，如果以点P为圆心的⊙P与直线BC相切，请用点P的横坐标x表示⊙P的半径R。

（3）在（2）的基础上判断⊙P与直线的位置关系。

Answer 1

【答案】（1）；（2）；（3）当时，⊙P与抛物线对称轴x=1相离，当时，⊙P与抛物线对称轴x=1相切，当时，⊙P与抛物线对称轴x=1相交.

【解析】试题分析： 分别令求得三点的坐标，即可用待定系数法求出直线的解析式.

设点D坐标为（）（0<x<4）,P(),进而表示出,

作于点M，延长PD交x轴于点H，先用勾股定理求出的长，用三角函数即可表示出的半径

分类讨论即可.

试题解析：（1）令中y=0，得，

，

解得： ，

易知

将B、C坐标分别代入，得解得： ，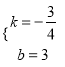

∴直线BC的解析式为： ；

（2）由题可设点D坐标为（）（0<x<4）,P(),

∴PD== ,(∵),

如图1，作于点M，延长PD交x轴于点H，则

，∴，

∴的半径 ，即；

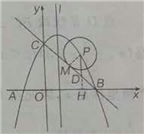
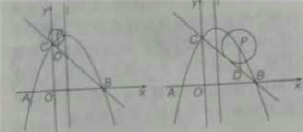
图1 图2 图3

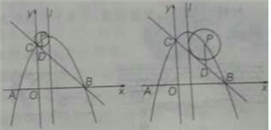
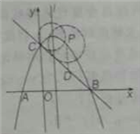
图4 图5 图6

（3）抛物线的对称轴是直线x=1，分类讨论：

①当与直线x=1在左侧相切（0<x<1），则，

整理得： ，解得： ，∵0<x<1，∴；

②当与直线在右侧相切（1<x<4），则，整理得： ，解得： ，∵1<x<4，∴；

综上所述，当或时， 与抛物线对称轴相离，如图2和图3所示；

当或时， 与抛物线对称轴相切，如图4和图5所示；

当时， 与抛物线对称轴相交，如图6所示.