题目内容
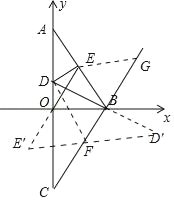
【题目】如图,直线y=﹣![]() x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
(1)求线段DE的长;
(2)一个动点P从点D出发,沿适当的路径运动到直线BC上的点F,再沿射线CB方向移动2![]() 个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
(3)将△ADE绕点A顺时针方向旋转,旋转角度α(0<α≤180°),在旋转过程中DE所在的直线分别与直线BC、直线AC相交于点M、点N,是否存在某一时刻使△CMN为等腰三角形,若存在,请求出CM的长,若不存在,请说明理由.

【答案】(1)1;(2)(![]() ,
,![]() );(3)6+
);(3)6+![]() ﹣3
﹣3![]() 或6+
或6+![]() +3
+3![]() 或2
或2![]() ﹣2或8
﹣2或8![]() .
.
【解析】
(1)想办法证明DE⊥AB,利用角平分线的性质定理证明DE=OD即可解决问题;
(2)过点E作EE′∥BC,点E′在x轴下方且EE′=2![]() ,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2
,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2![]() .此时D→F→G→E的路径最短.
.此时D→F→G→E的路径最短.
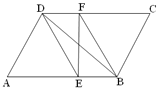
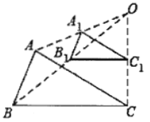
(3)分三种情形:①如图1中,当CM=CN时,在AE上取一点P,使得AP=PN.设EN=x.②如图2中,当MN=MC时,作BP⊥MN于P,则四边形ADPB是矩形.③如图3中,当NC=MN时,D与N重合,作DP⊥BC于P.分别解直角三角形即可解决问题.
解:(1)∵直线y=﹣![]() x+3与x轴相交于点B,与y轴相交于点A,
x+3与x轴相交于点B,与y轴相交于点A,
∴A(0,3),B(![]() ,0),
,0),
∴OA=3,OB=![]() ,
,
∴tan∠ABO=![]() =
=![]() ,
,
∴∠ABO=60°,
∵BD平分∠ABO,
∴∠DBO=30°,
∴OD=OBtan30°=1,DB=2OD=2,
∴AD=DB=2,
∴AE=EB,
∴DE⊥AB,∵DO⊥OB,DB平分∠ABO,
∴DE=DO=1.
(2)过点E作EE′∥BC,点E′在x轴下方且EE′=2![]() ,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2
,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2![]() .此时D→F→G→E的路径最短.
.此时D→F→G→E的路径最短.
∵E′(![]() ,
,![]() ),D′(2
),D′(2![]() ,﹣1),
,﹣1),
∴直线D′E′的解析式为![]() ,直线BC的解析式为y=
,直线BC的解析式为y=![]() x﹣3,
x﹣3,
由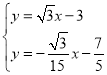 ,解得
,解得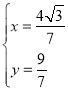 ,,
,,
∴F![]() .
.
把点F向上平移3个单位,向右平移![]() 个单位得到点G,
个单位得到点G,
∴G(![]() ).
).
(3)以点A为圆心,以AE为半径作⊙A,则DE为⊙A的切线.
①如图1中,当CM=CN时,在AE上取一点P,使得AP=PN.设EN=x.
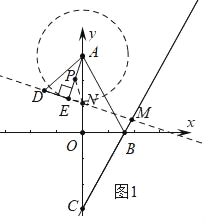
∵CM=CN,∠MCN=30°,
∴∠CNM=∠CMN=75°,
∴∠ANE=∠CNM=75°,
∴∠EAN=15°,
∴∠PAN=∠ANP=15°,
∴∠EPN=30°,
∴PN=AP=2x,PE=![]() x,
x,
∴2x+![]() x=
x=![]() ,
,
∴x=2![]() ﹣3,
﹣3,
∴AN=![]() ,
,
∴CM=CN=![]() =
=![]() .
.
②如图2中,当MN=MC时,作BP⊥MN于P,则四边形ADPB是矩形,PB=AE=![]() ,
,
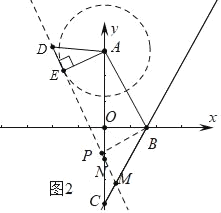
在Rt△PBM中,∠PBM=30°,
∴BM=2,
∴CM=BC﹣BM=2![]() ﹣2.
﹣2.
③如图2﹣1中.CM=CN时,同法可得CM=![]() .
.
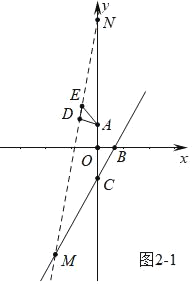
④如图3中,当NC=MN时,D与N重合,作DP⊥BC于P.
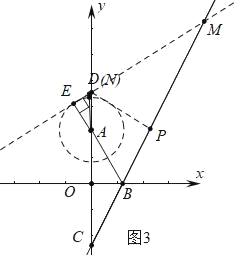
∵CD=6+2=8,∠DCP=30°,
∴PC=PM=4![]() ,
,
∴CM=8![]()
综上所述,满足条件的CM的值为![]() 或
或![]() 或2
或2![]() ﹣2或8
﹣2或8![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案