题目内容
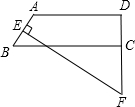如图，直角梯形的两底为AD=17cm，BC=25cm，斜腰AB=10cm，AB的垂直平分线EF交DC的延长线于F，求EF的长．
分析：根据线段的垂直平分线的性质可以连接AF，BF，则AF=BF．根据勾股定理，列出关于CF的方程进行求解，然后根据勾股定理计算BF的长，再进一步计算EF的长．
解答：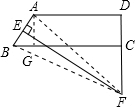
解：作AG⊥BC于G，连接BF，AF．
根据题意得：在直角三角形ABG中，AB=10，BG=25-17=8，
则AG=6，
所以CD=6．
因为EF垂直平分AB，
所以AF=BF．
设CF=x，
根据勾股定理得，252+x2=（x+6）2+172
解得：x=25．
在直角三角形BCF中，根据勾股定理，得BF=25
；
在直角三角形BEF中，根据勾股定理，得EF=35．
解：作AG⊥BC于G，连接BF，AF．根据题意得：在直角三角形ABG中，AB=10，BG=25-17=8，
则AG=6，
所以CD=6．
因为EF垂直平分AB，
所以AF=BF．
设CF=x，
根据勾股定理得，252+x2=（x+6）2+172
解得：x=25．
在直角三角形BCF中，根据勾股定理，得BF=25
| 2 |
在直角三角形BEF中，根据勾股定理，得EF=35．
点评：注意直角梯形中常见的辅助线是作另一高；此题中要熟练运用勾股定理．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图，直角梯形ABCD中，AD∥BC，∠B=90°，腰AB=4，两底之差为2，求另一腰CD的长．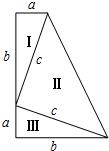
如图，三个直角三角形（Ⅰ，Ⅱ，Ⅲ）拼成一个直角梯形（两底分别为a、b，高为a+b），利用这个图形，小明验证了勾股定理．请你填写计算过程中留下的空格：
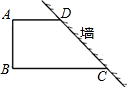，设AB=AD=x米，BC=y米，且x＜y．
如图，直角梯形的两底为AD=17cm，BC=25cm，斜腰AB=10cm，AB的垂直平分线EF交DC的延长线于F，求EF的长．