Question

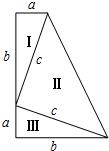如图，三个直角三角形（Ⅰ，Ⅱ，Ⅲ）拼成一个直角梯形（两底分别为a、b，高为a+b），利用这个图形，小明验证了勾股定理．请你填写计算过程中留下的空格：
S_梯形=

1

2

（上底+下底）•高=

1

2

（a+b）•（a+b），即S_梯形=

1

2

（

 

）①
S_梯形=Ⅰ+Ⅱ+Ⅲ（罗马数字表式相应图形的面积）
=

 

+

 

+

 

，即S_梯形=

1

2

（

 

）②
由①、②，得a²+b²=c²．

Answer 1

分析：此等腰梯形的面积有三部分组成，利用等腰梯形的面积等于三个直角三角形的面积之和列出方程并整理．

解答：解：因为S梯形=

1

2

(a+b)2=

1

2

(a2+2ab+b2)，
又因为S_梯形=Ⅰ+Ⅱ+Ⅲ=

1

2

ab+

1

2

c²+

1

2

ab=

1

2

(2ab+c2)，
所以

1

2

(a2+2ab+b2)=

1

2

(2ab+c2)，

1

2

a2+ab+

1

2

b2=ab+

1

2

c2
得c²=a²+b²．
故答案为：a²+2ab+b²，

1

2

ab，

1

2

c²，

1

2

ab，2ab+c²．

点评：本题考查了勾股定理的证明．此类证明要转化成该图形面积的两种表示方法，从而转化成方程达到证明的结果．