题目内容
 如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到0.1m,参考数据:
如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到0.1m,参考数据:| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:由题可知,在图中有两个直角三角形.在Rt△ACD中,利用30°角的正切求出CD;在Rt△ABD中,利用60°角的正切求出CD,二者相加即可.
解答: 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,
∵从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,
∴∠BAD=60°,∠DAC=30°,AD=66m,
∴tan60°=
,
∴BD=ADtan60°=66
(m),
∵tan30°=
,
∴CD=ADtan30°=22
(m),
∴BC=BD+CD=66
+22
=88
≈152.4(m),
答:这栋高楼的高度约为152.4m.
 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,∵从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,
∴∠BAD=60°,∠DAC=30°,AD=66m,
∴tan60°=
| BD |
| AD |
∴BD=ADtan60°=66
| 3 |
∵tan30°=
| CD |
| AD |
∴CD=ADtan30°=22
| 3 |
∴BC=BD+CD=66
| 3 |
| 3 |
| 3 |
答:这栋高楼的高度约为152.4m.
点评:此题主要考查了解直角三角形的应用,根据已知熟练掌握锐角三角函数关系得出CD,BD的长是解题关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
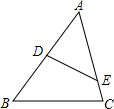 如图:在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,且AD:AC=2:3,那么DE:BC等于( )
如图:在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,且AD:AC=2:3,那么DE:BC等于( )| A、3:1 | B、1:3 |
| C、3:4 | D、2:3 |
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D. 如图,在△ABC中,∠C=90°,cosA=
如图,在△ABC中,∠C=90°,cosA= 如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,cosA=
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,cosA= 如图,一个半径为6cm,面积为127πcm2的扇形纸片,现需要一个半径为R的圆形纸片,使两张纸片刚好合成圆锥体,则R=
如图,一个半径为6cm,面积为127πcm2的扇形纸片,现需要一个半径为R的圆形纸片,使两张纸片刚好合成圆锥体,则R= 如图,在Rt△ABC中,已知∠ACB=90°,AC=1,BC=3,将△ABC绕着点A按逆时针方向旋转30°,使得点B与点B′重合,点C与点C′重合,则图中阴影部分的面积为
如图,在Rt△ABC中,已知∠ACB=90°,AC=1,BC=3,将△ABC绕着点A按逆时针方向旋转30°,使得点B与点B′重合,点C与点C′重合,则图中阴影部分的面积为