Question

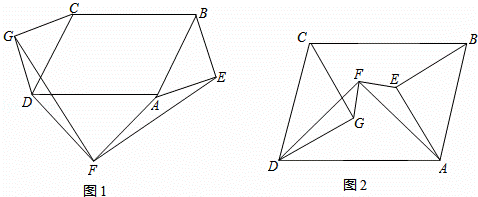
如图，MN是⊙O的直径，QN是⊙O的切线，连接MQ交⊙O于点H，E为上一点，连接ME，NE，NE交MQ于点F，且ME²=EF•EN．

（1）求证：QN=QF；

（2）若点E到弦MH的距离为1，cos∠Q=，求⊙O的半径．

Answer 1

（1）证明：如图1，

∵ME²=EF•EN，

∴=．

又∵∠MEF=∠MEN，

∴△MEF∽△MEN，

∴∠1=∠EMN．

∵∠1=∠2，∠3=∠EMN，

∴∠2=∠3，

∴QN=QF；

（2）解：如图2，连接OE交MQ于点G，设⊙O的半径是r．

由（1）知，△MEF∽△MEN，则∠4=∠5．

∴=．

∴OE⊥MQ，

∴EG=1．

∵cos∠Q=，且∠Q+∠GMO=90°，

∴sin∠GMO=，

∴=，即=，

解得，r=2.5，即⊙O的半径是2.5．