题目内容
20．
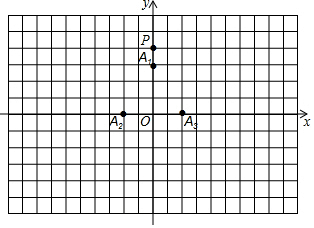如图，在平面直角坐标系xOy中，当A1（0，3）、A2（-2，0）、A3（2，0）为旋转中心时，点P（0，4）绕着点A1旋转180°得到P1点；点P1绕着点A2旋转180°得到P2点；点P2绕着点A3旋转180°得到P3点；点P3绕着点A1转180°得到点P4点…．继续如此操作若干次得到点P5、P6、…，则点P2的坐标为（-4，-2），点P2017的坐标为（0，2）．
分析 利用已知得出对应点坐标，进而得出P点坐标变换规律，进而得出答案．
解答 解：如图所示，点P2的坐标为：（-4，-2），
∵由图形可得出：P点与P6重合，
∴P点每6次循环一次，
∵2017÷6=336…1，
∴点P2017的坐标与P1坐标相同为：（0，2），
故答案为：（-4，-2），（0，2）．
点评 此题主要考查了几何变换以及点的坐标确定位置，得出P点坐标变化规律是解题关键．
练习册系列答案
相关题目
10．已知点（m，n）是正比例函数y=kx（k≠0）上的一点，当m增加2时，n就减小3，则k的值为（ ）
| A． | 2 | B． | -3 | C． | -$\frac{2}{3}$ | D． | -$\frac{3}{2}$ |
8．方程x2-121=0的根是（ ）
| A． | 11 | B． | -11 | C． | 11或-11 | D． | 14或-14 |
15．
如图，已知等边△ABC外有一点P，P落在∠BAC内，设P到BC、CA、AB的距离分别为h1，h2，h3，满足h2+h3-h1=6，那么等边△ABC的面积为（ ）
如图，已知等边△ABC外有一点P，P落在∠BAC内，设P到BC、CA、AB的距离分别为h1，h2，h3，满足h2+h3-h1=6，那么等边△ABC的面积为（ ）| A． | 4$\sqrt{3}$ | B． | 8$\sqrt{3}$ | C． | 9$\sqrt{3}$ | D． | 12$\sqrt{3}$ |
12．已知b＜0．则a，a-b，a+b中最大的是（ ）
| A． | a | B． | a+b | C． | a-b | D． | 以上都不对 |
9．
如图，在△ABC中，点D在边AB上，过点D作DE∥BC交AC于点E，DF∥AC交BC于F，若AE：DF=2：3，则BF：BC的值是（ ）
如图，在△ABC中，点D在边AB上，过点D作DE∥BC交AC于点E，DF∥AC交BC于F，若AE：DF=2：3，则BF：BC的值是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{5}$ |
10．下列说法正确的是（ ）
| A． | 单项式-$\frac{{x}^{2}}{3}$的系数是-3 | B． | 单项式2πa3的次数是4 | ||
| C． | 多项式x2y2-2x2+3是四次三项式 | D． | 多项式x2-2x+3的项分别是x2、2x、3 |