题目内容
在y=-2x2+4x+3中.
(1)写出该抛物线的增减性,顶点坐标,对称轴,开口方向和最大值;
(2)求出与y轴的交点C的坐标以及其对称点D的坐标;
(3)求出与x轴的交点A、B的坐标;
(4)写出当x为何值时,①y=0;②y>0;③y<0;
(5)写出当x为何值时,①y=3;②y>3;③y<3;
(6)已知(-5,y1)和(10,y2)比较y1和y2的大小;
(7)求四边形ABCD的面积;
(8)已知点M(3,-3),在x轴上找一P使得MP+CP的值最小,并写出点P的坐标;
(9)写出此抛物线向左平移两个单位长度再向下平移三个单位长度后的解析式.
(1)写出该抛物线的增减性,顶点坐标,对称轴,开口方向和最大值;
(2)求出与y轴的交点C的坐标以及其对称点D的坐标;
(3)求出与x轴的交点A、B的坐标;
(4)写出当x为何值时,①y=0;②y>0;③y<0;
(5)写出当x为何值时,①y=3;②y>3;③y<3;
(6)已知(-5,y1)和(10,y2)比较y1和y2的大小;
(7)求四边形ABCD的面积;
(8)已知点M(3,-3),在x轴上找一P使得MP+CP的值最小,并写出点P的坐标;
(9)写出此抛物线向左平移两个单位长度再向下平移三个单位长度后的解析式.
考点:二次函数综合题
专题:
分析:(1)根据二次函数的性质即可求解;
(2)将x=0代入y=-2x2+4x+3,求出y的值,进而得到与y轴的交点C的坐标,根据抛物线的对称性得到对称点D的坐标;
(3)将y=0代入y=-2x2+4x+3,求出x的值,进而得到与x轴的交点A、B的坐标;
(4)①A、B两点横坐标的值即为y=0时x的值;②二次函数y=-2x2+4x+3落在x轴上方的部分即为y>0时x的取值,根据抛物线开口方向及与x轴的交点A、B
横坐标的值即可求解;③二次函数y=-2x2+4x+3落在x轴下方的部分即为y<0时x的取值,根据抛物线开口方向及与x轴的交点A、B横坐标的值即可求解;
(5)①由于C、D两点纵坐标的值为3,所以C、D两点横坐标的值即为y=3x的值;②二次函数y=-2x2+4x+3落在CD上方的部分即为y>3时x的取值,根据抛物线开口方向及与C、D两点横坐标的值即可求解;③二次函数y=-2x2+4x+3落在CD下方的部分即为y<3时x的取值,根据抛物线开口方向及与C、D两点横坐标的值即可求解;
(6)把x=-5,x=10分别代入已知抛物线解析式,并分别求得y1与y2的值,然后比较它们的大小即可;
(7)根据四边形ABCD的面积=
(AB+CD)•OC即可求解;
(8)运用待定系数法求出直线CM的解析式,根据两点之间线段最短可知直线CM与x轴的交点的坐标即为点P的坐标;
(9)根据“左加右减,上加下减”的平移规律即可求解.
(2)将x=0代入y=-2x2+4x+3,求出y的值,进而得到与y轴的交点C的坐标,根据抛物线的对称性得到对称点D的坐标;
(3)将y=0代入y=-2x2+4x+3,求出x的值,进而得到与x轴的交点A、B的坐标;
(4)①A、B两点横坐标的值即为y=0时x的值;②二次函数y=-2x2+4x+3落在x轴上方的部分即为y>0时x的取值,根据抛物线开口方向及与x轴的交点A、B
横坐标的值即可求解;③二次函数y=-2x2+4x+3落在x轴下方的部分即为y<0时x的取值,根据抛物线开口方向及与x轴的交点A、B横坐标的值即可求解;
(5)①由于C、D两点纵坐标的值为3,所以C、D两点横坐标的值即为y=3x的值;②二次函数y=-2x2+4x+3落在CD上方的部分即为y>3时x的取值,根据抛物线开口方向及与C、D两点横坐标的值即可求解;③二次函数y=-2x2+4x+3落在CD下方的部分即为y<3时x的取值,根据抛物线开口方向及与C、D两点横坐标的值即可求解;
(6)把x=-5,x=10分别代入已知抛物线解析式,并分别求得y1与y2的值,然后比较它们的大小即可;
(7)根据四边形ABCD的面积=
| 1 |
| 2 |
(8)运用待定系数法求出直线CM的解析式,根据两点之间线段最短可知直线CM与x轴的交点的坐标即为点P的坐标;
(9)根据“左加右减,上加下减”的平移规律即可求解.
解答:解:(1)∵y=-2x2+4x+3=-2(x2-2x)+3=-2(x-1)2+5,
∴a=-2,
∴抛物线开口向下,
对称轴为直线x=1,顶点坐标为(1,5),最大值为5,
增减性:当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小;
(2)∵y=-2x2+4x+3,
∴当x=0时,y=3,∴C的坐标为(0,3),
∵对称轴为直线x=1,
∴对称点D的坐标为(2,3);
(3)∵y=-2x2+4x+3,
∴当y=0时,-2x2+4x+3=0,解得x=
,
∴点A的坐标为(
,0),点B的坐标为(
,0);
(4)①当x=
时,y=0;
②当
<x<
时,y>0;
③当x<
或x>
时,y<0;
(5)①∵C(0,3),D(2,3),
∴当x=0或2时,y=0;
②当0<x<2时,y>3;
③当x<0或x>2时,y<3;
 (6)∵y=-2x2+4x+3,
(6)∵y=-2x2+4x+3,
∴当x=-5时,y1=-2×(-5)2+4×(-5)+3=-67,
当x=10时,y2=-2×102+4×10+3=-157,
∴y1>y2;
(7)∵AB=
-
=
,CD=2,OC=3,
∴四边形ABCD的面积=
(AB+CD)•OC=
(
+2)×3=
;
 (8)设直线CM的解析式为y=kx+b,
(8)设直线CM的解析式为y=kx+b,
∵C(0,3),M(3,-3),
∴
,解得
,
∴y=-2x+3,
当y=0时,-2x+3=0,x=
,
∴点P的坐标为(
,0);
(9)∵y=-2x2+4x+3=-2(x-1)2+5,
∴将此抛物线向左平移两个单位长度再向下平移三个单位长度后的解析式为y=-2(x-1+2)2+5-3,即y=-2(x+1)2+2或y=-2x2-4x.
∴a=-2,
∴抛物线开口向下,
对称轴为直线x=1,顶点坐标为(1,5),最大值为5,
增减性:当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小;
(2)∵y=-2x2+4x+3,
∴当x=0时,y=3,∴C的坐标为(0,3),
∵对称轴为直线x=1,
∴对称点D的坐标为(2,3);
(3)∵y=-2x2+4x+3,
∴当y=0时,-2x2+4x+3=0,解得x=
2±
| ||
| 2 |
∴点A的坐标为(
2+
| ||
| 2 |
2-
| ||
| 2 |
(4)①当x=
2±
| ||
| 2 |
②当
2-
| ||
| 2 |
2+
| ||
| 2 |
③当x<
2-
| ||
| 2 |
2+
| ||
| 2 |
(5)①∵C(0,3),D(2,3),
∴当x=0或2时,y=0;
②当0<x<2时,y>3;
③当x<0或x>2时,y<3;
 (6)∵y=-2x2+4x+3,
(6)∵y=-2x2+4x+3,∴当x=-5时,y1=-2×(-5)2+4×(-5)+3=-67,
当x=10时,y2=-2×102+4×10+3=-157,
∴y1>y2;
(7)∵AB=
2+
| ||
| 2 |
2-
| ||
| 2 |
| 10 |
∴四边形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
3
| ||
| 2 |
 (8)设直线CM的解析式为y=kx+b,
(8)设直线CM的解析式为y=kx+b,∵C(0,3),M(3,-3),
∴
|
|
∴y=-2x+3,
当y=0时,-2x+3=0,x=
| 3 |
| 2 |
∴点P的坐标为(
| 3 |
| 2 |
(9)∵y=-2x2+4x+3=-2(x-1)2+5,
∴将此抛物线向左平移两个单位长度再向下平移三个单位长度后的解析式为y=-2(x-1+2)2+5-3,即y=-2(x+1)2+2或y=-2x2-4x.
点评:本题主要考查了二次函数的性质,二次函数图象上点的坐标特征,二次函数与方程、不等式的关系,待定系数法求一次函数的解析式,等腰梯形的面积,二次函数的图象与几何变换等知识,综合性较强,涉及的知识点较多,运用数形结合思想是解答此题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
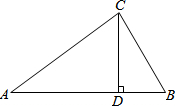 如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DC=12.
如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DC=12.