题目内容
在△ABC中,AB=AC=8,∠BAC=120°,取一把含30°角三角板,把30°角的顶点放在边BC的中点P处,三角板绕点P旋转.
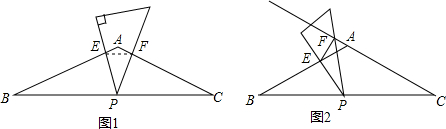
(1)如图1,当三角板的两边分别交边AB、AC于点E、F,连接EF,请说明△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图2情形时,三角板的两边分别交CA的延长线、边AB于点F、E,连接EF.
①探究1:△BPE与△CFP相似吗?请说明理由;
②探究2:△BPE与△PFE相似吗?请说明理由;
(3)设AE=x,EF=y,求y与x的函数分析式,并写出自变x的取值范围.

(1)如图1,当三角板的两边分别交边AB、AC于点E、F,连接EF,请说明△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图2情形时,三角板的两边分别交CA的延长线、边AB于点F、E,连接EF.
①探究1:△BPE与△CFP相似吗?请说明理由;
②探究2:△BPE与△PFE相似吗?请说明理由;
(3)设AE=x,EF=y,求y与x的函数分析式,并写出自变x的取值范围.
考点:相似形综合题
专题:综合题
分析:(1)已知∠B=∠C,要证△BPE∽△CFP,只需证到∠BEP=∠FPC即可.
(2)借鉴(1)中的解题经验即可证到△BPE∽△CFP,从而可得
=
,由BP=CP可得
=
,再由∠B=∠EPF=30°就可得到△BPE∽△PFE.
(3)连接AP,过点P作PD⊥AB于D,由△BPE∽△PFE(已证)可得BE•FE=PE2,其中BE=8-x,FE=y,只需在Rt△PDE中运用勾股定理用x的代数式表示出PE2,就可解决问题.
(2)借鉴(1)中的解题经验即可证到△BPE∽△CFP,从而可得
| BE |
| CP |
| PE |
| FP |
| BE |
| BP |
| PE |
| FP |
(3)连接AP,过点P作PD⊥AB于D,由△BPE∽△PFE(已证)可得BE•FE=PE2,其中BE=8-x,FE=y,只需在Rt△PDE中运用勾股定理用x的代数式表示出PE2,就可解决问题.
解答:解:(1)证明:如图1,
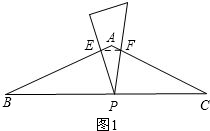
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵∠EPC=∠B+∠BEP=∠EPF+∠FPC,∠B=∠EPF=30°,
∴∠BEP=∠FPC,
∴△BPE∽△CFP.
(2)①△BPE∽△CFP.
证明:如图2,

∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵∠EPC=∠B+∠BEP=∠EPF+∠FPC,∠B=∠EPF=30°,
∴∠BEP=∠FPC,
∴△BPE∽△CFP.
②△BPE∽△PFE.
证明:∵△BPE∽△CFP,
∴
=
.
∵BP=CP,
∴
=
.
∵∠B=∠EPF=30°,
∴△BPE∽△PFE.
(3)连接AP,过点P作PD⊥AB于D,如图3,
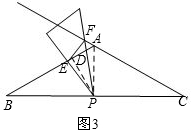
∵AB=AC,P为BC中点,
∴AP⊥BC.
∵∠B=30°,
∴AP=
AB=4,
∴BP=
=4
.
∴PD=
BP=2
,
∴BD=
=6,
∴DE=|BD-BE|=|6-(8-x)|=|x-2|,
∴PE2=PD2+DE2=(2
)2+(x-2)2=x2-4x+16.
∵△BPE∽△PFE(已证),
∴
=
,
∴BE•FE=PE2,
∴(8-x)•y=x2-4x+16
∴y=
(0≤x<8).

∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵∠EPC=∠B+∠BEP=∠EPF+∠FPC,∠B=∠EPF=30°,
∴∠BEP=∠FPC,
∴△BPE∽△CFP.
(2)①△BPE∽△CFP.
证明:如图2,

∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵∠EPC=∠B+∠BEP=∠EPF+∠FPC,∠B=∠EPF=30°,
∴∠BEP=∠FPC,
∴△BPE∽△CFP.
②△BPE∽△PFE.
证明:∵△BPE∽△CFP,
∴
| BE |
| CP |
| PE |
| FP |
∵BP=CP,
∴
| BE |
| BP |
| PE |
| FP |
∵∠B=∠EPF=30°,
∴△BPE∽△PFE.
(3)连接AP,过点P作PD⊥AB于D,如图3,

∵AB=AC,P为BC中点,
∴AP⊥BC.
∵∠B=30°,
∴AP=
| 1 |
| 2 |
∴BP=
| AB2-AP2 |
| 3 |
∴PD=
| 1 |
| 2 |
| 3 |
∴BD=
| BP2-PD2 |
∴DE=|BD-BE|=|6-(8-x)|=|x-2|,
∴PE2=PD2+DE2=(2
| 3 |
∵△BPE∽△PFE(已证),
∴
| BE |
| PE |
| PE |
| FE |
∴BE•FE=PE2,
∴(8-x)•y=x2-4x+16
∴y=
| x2-4x+16 |
| 8-x |
点评:本题考查了相似三角形的判定与性质、等腰三角形的性质、30°角所对的直角边等于斜边的一半、勾股定理等知识,由△BPE∽△PFE得到BE•FE=PE2是解决第(3)小题的关键.

练习册系列答案
相关题目