题目内容
 如图是用矩形ABCD做成的飞镖板,其中AB=4,AE=2,ED=3.小明和小聪距飞镖板一定距离向飞镖板投掷飞镖(假设他们投掷的飞镖均扎在飞镖板上),如果飞镖落在阴影M区域内小明胜,落在阴影N区域内小聪胜,这样决胜负公平吗?判断并说明理由,如果不公平,利用这个飞镖板,在图形不变的情况下,请设计一个对双方都公平的游戏规则.
如图是用矩形ABCD做成的飞镖板,其中AB=4,AE=2,ED=3.小明和小聪距飞镖板一定距离向飞镖板投掷飞镖(假设他们投掷的飞镖均扎在飞镖板上),如果飞镖落在阴影M区域内小明胜,落在阴影N区域内小聪胜,这样决胜负公平吗?判断并说明理由,如果不公平,利用这个飞镖板,在图形不变的情况下,请设计一个对双方都公平的游戏规则.分析:首先根据题意可求得小明胜与小聪胜的概率,比较概率大小,即可确定是否公平.双方获胜的概率相同,就公平,否则不公平.
解答:解:不公平.理由:
∵矩形ABCD中,AB=4,AE=2,ED=3,
∴AD=AE+DE=5,
∴S阴影M=
AE×AB=
×2×4=4,S阴影N=
DE×AB=
×3×4=6,S四边形ABCD=AD•AB=5×4=20,
∴P(小明胜)=
=
=
,P(小聪胜)=
=
=
,
∵P(小明胜)≠P(小聪胜),
∴不公平.
设计方案:如果飞镖落在阴影区域内小明胜,落在非阴影区域内小聪胜.
∵矩形ABCD中,AB=4,AE=2,ED=3,
∴AD=AE+DE=5,
∴S阴影M=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴P(小明胜)=
| S阴影M |
| S四边形ABCD |
| 4 |
| 20 |
| 1 |
| 5 |
| S阴影N |
| S四边形ABCD |
| 6 |
| 20 |
| 3 |
| 10 |
∵P(小明胜)≠P(小聪胜),
∴不公平.
设计方案:如果飞镖落在阴影区域内小明胜,落在非阴影区域内小聪胜.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
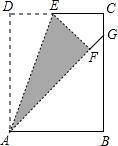 (2013•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若
(2013•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若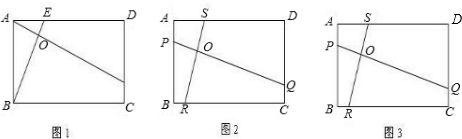
 如图是用矩形ABCD做成的飞镖板,其中AB=4,AE=2,ED=3.小明和小聪距飞镖板一定距离向飞镖板投掷飞镖(假设他们投掷的飞镖均扎在飞镖板上),如果飞镖落在阴影M区域内小明胜,落在阴影N区域内小聪胜,这样决胜负公平吗?判断并说明理由,如果不公平,利用这个飞镖板,在图形不变的情况下,请设计一个对双方都公平的游戏规则.
如图是用矩形ABCD做成的飞镖板,其中AB=4,AE=2,ED=3.小明和小聪距飞镖板一定距离向飞镖板投掷飞镖(假设他们投掷的飞镖均扎在飞镖板上),如果飞镖落在阴影M区域内小明胜,落在阴影N区域内小聪胜,这样决胜负公平吗?判断并说明理由,如果不公平,利用这个飞镖板,在图形不变的情况下,请设计一个对双方都公平的游戏规则.