题目内容
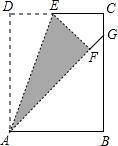 (2013•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若
(2013•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若| CG |
| GB |
| 1 |
| k |
| AD |
| AB |
| ||
| 2 |
| ||
| 2 |
分析:根据中点定义可得DE=CE,再根据翻折的性质可得DE=EF,AF=AD,∠AFE=∠D=90°,从而得到CE=EF,连接EG,利用“HL”证明Rt△ECG和Rt△EFG全等,根据全等三角形对应边相等可得CG=FG,设CG=a,表示出GB,然后求出BC,再根据矩形的对边相等可得AD=BC,从而求出AF,再求出AG,然后利用勾股定理列式求出AB,再求比值即可.
解答: 解:∵点E是边CD的中点,
解:∵点E是边CD的中点,
∴DE=CE,
∵将△ADE沿AE折叠后得到△AFE,
∴DE=EF,AF=AD,∠AFE=∠D=90°,
∴CE=EF,
连接EG,
在Rt△ECG和Rt△EFG中,
,
∴Rt△ECG≌Rt△EFG(HL),
∴CG=FG,
设CG=a,∵
=
,
∴GB=ka,
∴BC=CG+BG=a+ka=a(k+1),
在矩形ABCD中,AD=BC=a(k+1),
∴AF=a(k+1),
AG=AF+FG=a(k+1)+a=a(k+2),
在Rt△ABG中,AB=
=
=2a
,
∴
=
=
.
故答案为:
.
 解:∵点E是边CD的中点,
解:∵点E是边CD的中点,∴DE=CE,
∵将△ADE沿AE折叠后得到△AFE,
∴DE=EF,AF=AD,∠AFE=∠D=90°,
∴CE=EF,
连接EG,
在Rt△ECG和Rt△EFG中,
|
∴Rt△ECG≌Rt△EFG(HL),
∴CG=FG,
设CG=a,∵
| CG |
| GB |
| 1 |
| k |
∴GB=ka,
∴BC=CG+BG=a+ka=a(k+1),
在矩形ABCD中,AD=BC=a(k+1),
∴AF=a(k+1),
AG=AF+FG=a(k+1)+a=a(k+2),
在Rt△ABG中,AB=
| AG2-BG2 |
| [a(k+2)]2-(ka)2 |
| k+1 |
∴
| AD |
| AB |
| a(k+1) | ||
2a
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了矩形的性质,全等三角形的判定与性质,勾股定理的应用,以及翻折变换的性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
 (2013•苏州)如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(2013•苏州)如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向. (2013•苏州)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P.则点P的坐标为
(2013•苏州)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P.则点P的坐标为 (2013•苏州)如图,AB是半圆的直径,点D是
(2013•苏州)如图,AB是半圆的直径,点D是
 (2013•苏州)如图,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA,劣弧
(2013•苏州)如图,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA,劣弧