题目内容
在一个平面直角坐标系中，点A的坐标为（3，2），点B的坐标为（2，3），那么，请你画出一个平面直角坐标系，并标出点A，B两个点，且在标出点C，使△ABC为等腰直角三角形．
考点：勾股定理的逆定理,坐标与图形性质,勾股定理,等腰直角三角形
专题：
分析：分别从当∠ABC=90°，AB=BC时；当∠BAC=90°，AB=AC时；与当∠ACB=90°，AC=BC时去分析求解，利用网格结构，即可求得点C的坐标．
解答：
解：如图，分三种情况：
当∠ABC=90°，AB=BC时，点C的坐标为C1（1，2），C2（3，4）；
当∠BAC=90°，AB=AC时，点C的坐标为C3（2，1），C4（4，3）；
当∠ACB=90°，AC=BC时，点C的坐标为C5（2，2），C6（3，3）；
综上可得：点C的坐标为：C1（1，2），C2（3，4），C3（2，1），C4（4，3），C5（2，2），C6（3，3）．
解：如图，分三种情况：当∠ABC=90°，AB=BC时，点C的坐标为C1（1，2），C2（3，4）；
当∠BAC=90°，AB=AC时，点C的坐标为C3（2，1），C4（4，3）；
当∠ACB=90°，AC=BC时，点C的坐标为C5（2，2），C6（3，3）；
综上可得：点C的坐标为：C1（1，2），C2（3，4），C3（2，1），C4（4，3），C5（2，2），C6（3，3）．
点评：本题考查了等腰直角三角形，坐标与图形性质，利用数形结合及网格结构是解题的关键．
练习册系列答案
相关题目
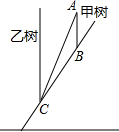由于大风，山坡上的一棵树甲被从点A处拦腰折断，如图，树甲恰好落在另一棵树乙的根部C处，已知AB=1米，BC=5米，已知两棵树的水平距离为3米，这棵树原来的高度为