题目内容
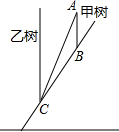 由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,树甲恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,这棵树原来的高度为
由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,树甲恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,这棵树原来的高度为考点:勾股定理的应用
专题:
分析:过作CD⊥AB交AB延长线于D,根据勾股定理求得BD的长,从而求得线段AD的长,然后根据勾股定理求得AC的长,从而求得线段AC的长.
解答: 解:如图作CD⊥AB交AB延长线于D,
解:如图作CD⊥AB交AB延长线于D,
由题意知BC=5,CD=3,
根据勾股定理得:BD=4,
∵AB=1,
∴AD=5,
∴AC=
=
,
∴这棵树原来的高度=AB+AC=(1+
)m.
 解:如图作CD⊥AB交AB延长线于D,
解:如图作CD⊥AB交AB延长线于D,由题意知BC=5,CD=3,
根据勾股定理得:BD=4,
∵AB=1,
∴AD=5,
∴AC=
| 32+52 |
| 34 |
∴这棵树原来的高度=AB+AC=(1+
| 34 |
点评:本题考查了勾股定理的应用,考查了实数大小的比较,本题中正确的计算AC,AB的长是解题的关键.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠BDC=
如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠BDC=