题目内容
 26、如图是边长为a+2b的正方形
26、如图是边长为a+2b的正方形(1)边长为a的正方形有
1
个(2)边长为b的正方形有
4
个(3)两边分别为a和b的矩形有
4
个(4)用不同的形式表示边长为a+2b的正方形面积,并进行比较写出你的结论.
分析:(1)(2)(3)根据图直接可以看出,(4)根据正方形的面积公式=边长×边长=(a+2b)(a+2b)=(a+2b)2,然后利用平方差公式把它展开又是另一种表现形式.
解答:解:(1)由图可知边长为a的正方形只有一个;
(2)由图可知边长为b的正方形有4个;
(3)由图可知两边长分别为a和b的矩形有4个;
(4)∵S边长为a+2b的正方形=(a+2b)2
S边长为a+2b的正方形=a2+4b2+4ab;
∴结论是(a+2b)2=a2+4b2+4ab.
(2)由图可知边长为b的正方形有4个;
(3)由图可知两边长分别为a和b的矩形有4个;
(4)∵S边长为a+2b的正方形=(a+2b)2
S边长为a+2b的正方形=a2+4b2+4ab;
∴结论是(a+2b)2=a2+4b2+4ab.
点评:本题主要考查了同学们的观察能力以及运用面积公式求正方形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
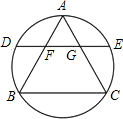 如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )
如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( ) 如图是边长为a+2b的正方形
如图是边长为a+2b的正方形
