Question

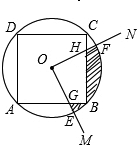
如图，已知：⊙O的直径AB与弦AC的夹角∠A=30°，过点C作⊙O的切线交AB的延长线于点P．
（1）求证：AC=CP；
（2）若PC=6，求图中阴影部分的面积（结果精确到0.1）．
（参考数据：

3

=1.73，π=3.14）

Answer 1

（1）证明：连接OC．
∵AB是⊙O的直径，
∴AO=OC，
∴∠ACO=∠A=30°．
∴∠COP=2∠ACO=60°．
∵PC切⊙O于点C，
∴OC⊥PC．
∴∠P=30°．
∴∠A=∠P．
∴AC=PC．

（2）在Rt△OCP中，tan∠P=

OC

CP

，∴OC=2

3

∵S_△OCP=

1

2

CP•OC=

1

2

×6×2

3

=6

3

且S_扇形COB=2π，
∴S_阴影=S_△OCP-S_扇形COB=6

3

-2π≈4.1．