题目内容
8.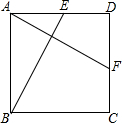 如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
分析 根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE和△ADF全等,根据全等三角形对应边相等证明即可.
解答 证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠D=90°}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴BE=AF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,以及垂直的定义,求出两三角形全等,从而得到BE=AF是解题的关键.

练习册系列答案
相关题目
19.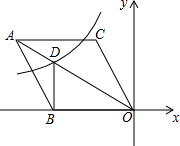 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )| A. | 6$\sqrt{3}$ | B. | -6$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | -12$\sqrt{3}$ |
3.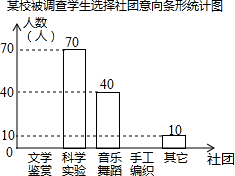 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
13.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )


| A. | 21 | B. | 24 | C. | 27 | D. | 30 |
18.一次函数y=-2x+1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
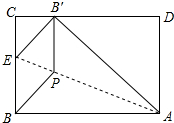 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论:
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论: 已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.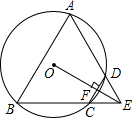 如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.