题目内容
【题目】如图，直线y＝﹣
x＋4与x轴、y轴分别交于点A、B、C是线段AB上一点，四边形OADC是菱形，则OD的长为（ ）
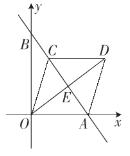
A. 4.2B. 4.8C. 5.4D. 6
【答案】B
【解析】
由直线的解析式可求出点B、A的坐标，进而可求出OA、OB的长，再利用勾股定理即可求出AB的长，由菱形的性质可得OE⊥AB，OE=DE，再根据直角三角形的面积可求出OE的长，进而可求出OD的长.
解：∵直线y＝﹣
x＋4与x轴、y轴分别交于点A、B，
∴点A（3,0）、点B（0,4），
∴OA=3，OB=4，
∴AB=
，
∵四边形OADC是菱形,
∴OE⊥AB，OE=DE，
由直角三角形的面积得
，
即3×4=5×OE.
解得：OE=2.4，
∴OD=2OE=4.8.
故选B.
练习册系列答案
相关题目
【题目】某客运站行车时刻表如图，若全程保持匀速行驶，则当快车出发______小时后，两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程（km） |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |
