Question

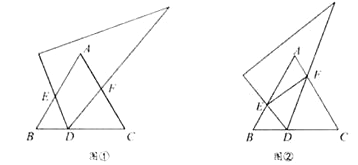
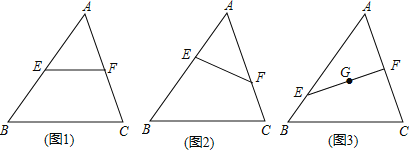
【题目】在△ABC中，E、F分别为线段AB、AC上的点（不与A、B、C重合）．

（1）如图1，若EF∥BC，求证：

（2）如图2，若EF不与BC平行，（1）中的结论是否仍然成立？请说明理由；

（3）如图3，若EF上一点G恰为△ABC的重心，，求的值．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）

【解析】（1）由EF∥BC知△AEF∽△ABC，据此得，根据即可得证；

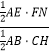（2）分别过点F、C作AB的垂线，垂足分别为N、H，据此知△AFN∽△ACH，得，根据=即可得证；

（3）连接AG并延长交BC于点M，连接BG并延长交AC于点N，连接MN，由重心性质知S△ABM=S△ACM、=，设=a，利用（2）中结论知==、==a，从而得==+a，结合==a可关于a的方程，解之求得a的值即可得出答案．

（1）∵EF∥BC，

∴△AEF∽△ABC，

∴，

∴==；

（2）若EF不与BC平行，（1）中的结论仍然成立，

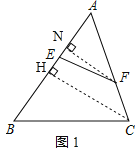
分别过点F、C作AB的垂线，垂足分别为N、H，

∵FN⊥AB、CH⊥AB，

∴FN∥CH，

∴△AFN∽△ACH，

∴，

∴==；

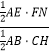（3）连接AG并延长交BC于点M，连接BG并延长交AC于点N，连接MN，

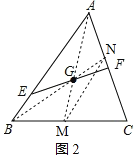
则MN分别是BC、AC的中点，

∴MN∥AB，且MN=AB，

∴=，且S△ABM=S△ACM，

∴=，

设=a，

由（2）知：==×=，==a，

则===+a，

而==a，

∴+a =a，

解得：a=，

∴=×=．