题目内容
9. 如图,直线y=-x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=-x+10在第一象限内一个动点.
如图,直线y=-x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=-x+10在第一象限内一个动点.(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
分析 (1)根据三角形的面积公式S△OPA=$\frac{1}{2}$OA•y,然后把y转换成x,即可求得△OPA的面积S与x的函数关系式;
(2)把s=10代入S=-4x+40,求得x的值,把x的值代入y=-x+10即可求得P的坐标.
解答 解(1)∵A(8,0),
∴OA=8,
S=$\frac{1}{2}$OA•|yP|=$\frac{1}{2}$×8×(-x+10)=-4x+40,(0<x<10).
(2)当S=10时,则-4x+40=10,解得x=$\frac{15}{2}$,
当x=$\frac{15}{2}$时,y=-$\frac{15}{2}$+10=$\frac{5}{2}$,
∴当△OPA的面积为10时,点P的坐标为($\frac{15}{2}$,$\frac{5}{2}$).
点评 本题考查了一次函数图象上点的坐标特征和一次函数的性质,把求三角形的面积和一次函数的图象结合起来,综合性比较强.

练习册系列答案
相关题目
19.用配方法将x2-2x-2=0变形,正确的是( )
| A. | (x-1)2=1 | B. | (x+1)2=3 | C. | (x-1)2=3 | D. | (x+1)2=1 |
4.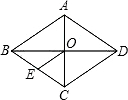 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
 如图,等腰△ABC的周长为19,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为12.
如图,等腰△ABC的周长为19,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为12.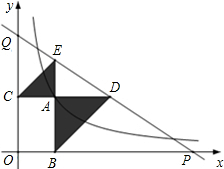 如图,已知动点A在函数y=$\frac{4}{x}$(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于$\frac{68}{15}$.
如图,已知动点A在函数y=$\frac{4}{x}$(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于$\frac{68}{15}$.