题目内容
如图,某一拦水坝的横断面为梯形ABCD,AD∥BC,斜坡AB的长10| 2 |
 宽16米,坝高10米,斜面CD的坡比i=1:
宽16米,坝高10米,斜面CD的坡比i=1:| 3 |
求:(1)坡角α和β;
(2)拦水坝横断面面积(结果保留根号)
分析:(1)已知了坡面CD的坡度,即β的正切值,由此可求得β的度数;过B作AD的垂线,设垂足为E,在Rt△ABE中,已知了AB、BE的长,可用α的正弦值求出α的度数.
(2)过C作CF⊥AD于F,根据CF的长以及坡面CD的坡比,可求得DF的长,即可求出AD的长,由此可根据梯形的面积公式求出拦水坝横断面的面积.
(2)过C作CF⊥AD于F,根据CF的长以及坡面CD的坡比,可求得DF的长,即可求出AD的长,由此可根据梯形的面积公式求出拦水坝横断面的面积.
解答: 解:(1)∵坡面CD的坡度为i=
解:(1)∵坡面CD的坡度为i=
,
∴tanβ=
,即∠β=30°;
过B作BE⊥AD于E;
在Rt△ABE中,sinα=
=
=
;
∴∠α=45°.
(2)过C作CF⊥AD于F;
在Rt△DCF中,i=
=
,CF=10m;
∴DF=10
m;
∴AD=AE+EF+DF=10+16+10
=26+10
m;
∴S梯形=
×(AD+BC)×BE=210+50
m2;
即拦水坝横断面的面积为210+50
m2.
 解:(1)∵坡面CD的坡度为i=
解:(1)∵坡面CD的坡度为i=| 1 | ||
|
∴tanβ=
| ||
| 3 |
过B作BE⊥AD于E;
在Rt△ABE中,sinα=
| BE |
| AB |
| 10 | ||
10
|
| ||
| 2 |
∴∠α=45°.
(2)过C作CF⊥AD于F;
在Rt△DCF中,i=
| CF |
| DF |
| 1 | ||
|
∴DF=10
| 3 |
∴AD=AE+EF+DF=10+16+10
| 3 |
| 3 |
∴S梯形=
| 1 |
| 2 |
| 3 |
即拦水坝横断面的面积为210+50
| 3 |
点评:此类应用问题尽管题型千变万化,但关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.

练习册系列答案
相关题目
 31、如图,某水库大坝的横断面是等腰梯形,坝顶宽6米,坝高10米.斜坡AB的坡度为1:2(AR:BR).现要加高2米,在坝顶宽度和斜坡坡度均不变的情况下,加固一条长为50米的大坝,需要多少土方.
31、如图,某水库大坝的横断面是等腰梯形,坝顶宽6米,坝高10米.斜坡AB的坡度为1:2(AR:BR).现要加高2米,在坝顶宽度和斜坡坡度均不变的情况下,加固一条长为50米的大坝,需要多少土方.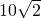 米,坝顶
米,坝顶 宽16米,坝高10米,斜面CD的坡比i=1:
宽16米,坝高10米,斜面CD的坡比i=1: .
. 如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是米.
如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是米. 米,坝顶宽16米,坝高10米,斜面CD的坡比i=1:
米,坝顶宽16米,坝高10米,斜面CD的坡比i=1: .
.