题目内容
3.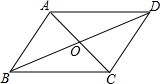 如图,在四边形ABCD中,AB∥DC,AD∥BC,对角线AC、BD相交于点O,则图中的一对全等三角形为△ABC≌△ADC.(写出一对即可)
如图,在四边形ABCD中,AB∥DC,AD∥BC,对角线AC、BD相交于点O,则图中的一对全等三角形为△ABC≌△ADC.(写出一对即可)
分析 利用ASA判定△ABC≌△ADC,再用AAS判定△ABO≌△CDO,再利用AAS定理判定△BCO≌△DAO.
解答 解:△ABC≌△ADC,理由如下:
∵AB∥DC,AD∥BC,
∴∠BAC=∠DCA,∠DAC=∠BCA,
在△ABC与△ADC中,
$\left\{\begin{array}{l}{∠BAC=∠DCA}\\{AC=CA}\\{∠DAC=∠BCA}\end{array}\right.$,
∴△ABC≌△ADC(ASA),
∴AB=DC,BC=DA,
在△ABO与△CDO中,
$\left\{\begin{array}{l}{∠BAO=∠DCO}\\{∠AOB=∠COD}\\{AB=DC}\end{array}\right.$,
∴△ABO≌△CDO(AAS),
同理可得:△BCO≌△DAO,
故答案为:△ABC≌△ADC
点评 此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
14. 若用a表示$\sqrt{8}$,则在数轴上与a-1最接近的数所表示的点是( )
若用a表示$\sqrt{8}$,则在数轴上与a-1最接近的数所表示的点是( )
 若用a表示$\sqrt{8}$,则在数轴上与a-1最接近的数所表示的点是( )
若用a表示$\sqrt{8}$,则在数轴上与a-1最接近的数所表示的点是( )| A. | A | B. | B | C. | C | D. | D |
18.把多项式3a2-9ab分解因式,正确的是( )
| A. | 3(a2-3ab) | B. | 3a(a-3b) | C. | a(3a-9b) | D. | a(9b-3a) |
15.下列方程是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{x^2}$+x=2 | C. | x2+2x=x2-1 | D. | 3x2+1=2x+2 |
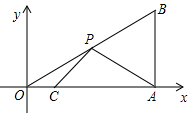 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,$\sqrt{3}$),点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,求PA+PC的最小值.
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,$\sqrt{3}$),点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,求PA+PC的最小值.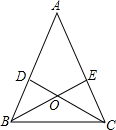 如图,在△ABC中,AB=AC,∠ABC的平分线BE与AC交于点E,∠ACB的平分线CD与AB交于点D,BE与CD相交于点O,求证:OB=OC,OD=OE.
如图,在△ABC中,AB=AC,∠ABC的平分线BE与AC交于点E,∠ACB的平分线CD与AB交于点D,BE与CD相交于点O,求证:OB=OC,OD=OE.


