题目内容
8.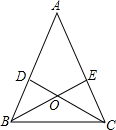 如图,在△ABC中,AB=AC,∠ABC的平分线BE与AC交于点E,∠ACB的平分线CD与AB交于点D,BE与CD相交于点O,求证:OB=OC,OD=OE.
如图,在△ABC中,AB=AC,∠ABC的平分线BE与AC交于点E,∠ACB的平分线CD与AB交于点D,BE与CD相交于点O,求证:OB=OC,OD=OE.
分析 首先根据等边对等角可得∠ABC=∠ACB,然后根据角平分线的性质可得∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,进而得到∠OBC=∠OCB,再根据等角对等边可得BO=CO;证明△BCD≌△CBE,得到CD=BE,即可得到OD=OE.
解答 解:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是角平分线,它们相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC=∠OCB,
∴BO=CO,
在△BCD和△CBE中,
$\left\{\begin{array}{l}{∠ABC=∠ACB}\\{BC=CB}\\{∠DCB=∠EBC}\end{array}\right.$,
∴△BCD≌△CBE,
∴CD=BE,
∴CD-OC=BE-OB,
∴OD=OE.
点评 本题考查了全等三角形的性质与判定、等腰三角形的性质、角平分线,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
18.下列不等式,是一元一次不等式的是( )
| A. | x+y<x+2 | B. | x2-2x-1 | C. | $\frac{1}{2}$$+\frac{1}{3}$>$\frac{1}{6}$ | D. | 2(1-y)+y>4y+2 |
16.计算a7•a3的结果是( )
| A. | a4 | B. | a10 | C. | a21 | D. | a73 |
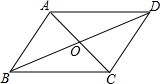 如图,在四边形ABCD中,AB∥DC,AD∥BC,对角线AC、BD相交于点O,则图中的一对全等三角形为△ABC≌△ADC.(写出一对即可)
如图,在四边形ABCD中,AB∥DC,AD∥BC,对角线AC、BD相交于点O,则图中的一对全等三角形为△ABC≌△ADC.(写出一对即可)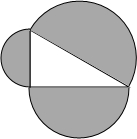 分别以直角三角形的三边为直径作半圆,则这三个半圆面积之间有什么样的关系,请加以说明.
分别以直角三角形的三边为直径作半圆,则这三个半圆面积之间有什么样的关系,请加以说明. 如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是15cm,求AB和AC的长.
如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是15cm,求AB和AC的长.