题目内容
8.在圆内接四边形ABCD中,∠A、∠B、∠C的度数之比为3:4:6,则∠D=100度.分析 根据圆内接四边形对角互补可得∠B+∠D=∠A+∠C=180°,再根据∠A、∠B、∠C的度数之比为3:4:6分别计算出∠A、∠B、∠C的度数,进而可得∠D的度数.
解答  解:∵四边形ABCD是圆内接四边形,
解:∵四边形ABCD是圆内接四边形,
∴∠B+∠D=∠A+∠C=180°,
∵∠A、∠B、∠C的度数之比为3:4:6,
∴∠A=180°×$\frac{3}{9}$=60°,∠C=180°×$\frac{6}{9}$=120°,
∠B=180°×$\frac{4}{9}$=80°,
∴∠D=180°-80°=100°,
故答案为:100.
点评 此题主要考查了圆内接四边形的性质,关键是掌握圆内接四边形对角互补.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.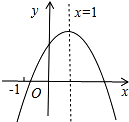 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),
其中正确的结论有( )
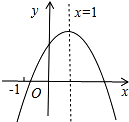 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 已知有理数a,b在数轴上所表示的点如图所示,则下列判断不正确的是( )
已知有理数a,b在数轴上所表示的点如图所示,则下列判断不正确的是( )
 已知有理数a,b在数轴上所表示的点如图所示,则下列判断不正确的是( )
已知有理数a,b在数轴上所表示的点如图所示,则下列判断不正确的是( )| A. | a,b异号 | B. | a有可能是整数 | ||
| C. | a的相反数大于b的相反数 | D. | 若a=-2,则b可能为-1 |
16.已知点P1(a,2013)和P2(-2012,b)关于原点对称,则(a+b)2014的值为( )
| A. | 1 | B. | -1 | C. | 72014 | D. | -72014 |
 如图,E、F分别为线段AC上两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于M.说明:MB=MD,ME=MF.
如图,E、F分别为线段AC上两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于M.说明:MB=MD,ME=MF.