题目内容
18.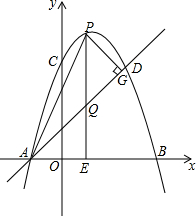 如图,抛物线y=-x2+bx+c 经过A(-1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.
如图,抛物线y=-x2+bx+c 经过A(-1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.(1)求抛物线的解析式;
(2)求点D的坐标及直线AD的解析式;
(3)当点P在直线AD上方时,求d关于m的函数关系式,并求出d的最大值;
(4)当点P在直线AD上方时,若PQ将△APG分成面积相等的两部分,直接写出m的值.
分析 (1)根据待定系数法可求抛物线的解析式;
(2)将y=-x2+2x+3配方得抛物线的对称轴,根据轴对称的性质可得点D的坐标,再根据待定系数法可求直线AD的解析式;
(3)根据两点间的距离公式可得d=-m2+2m+3-m-1=-m2+m+2=-(m-$\frac{1}{2}$)2+$\frac{9}{4}$,依此可求d的最大值;
(4)可设直线PG的解析式为y=-x+P,根据中点坐标公式可得G的坐标,再根据待定系数法可求m的值.
解答 解:(1)∵抛物线y=-x2+bx+c 经过A(-1,0),C(0,3)两点,
∴$\left\{\begin{array}{l}{-(-1)^{2}-b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
∴抛物线的解析式为y=-x2+2x+3.
(2)∵将y=-x2+2x+3配方,得y=-(x-1)2+4,
∴抛物线的对称轴是直线x=1.
∴点D的坐标为(2,3).
设直线AD的解析式为y=kx+n,
由题意,得$\left\{\begin{array}{l}{2k+n=3}\\{-k+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{n=1}\end{array}\right.$.
∴直线AD的解析式为y=x+1.
(3)∵点P的横坐标为m,
∴点P,Q的纵坐标分别为-m2+2m+3,m+1,
∴d=-m2+2m+3-m-1=-m2+m+2=-(m-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴d关于m函数关系式是d=-m2+m+2,d的最大值为$\frac{9}{4}$.
(4)设直线PG的解析式为y=-x+P,
∵PQ将△APG分成面积相等的两部分,
∴G的坐标为(2m+1,2m+2),
∴$\left\{\begin{array}{l}{-(2m+1)+p=2m+2}\\{-m+p=-{m}^{2}+2m+3}\end{array}\right.$,
解得m1=0,m2=-1(不合题意舍去).
故m的值为0.
点评 考查了二次函数综合题,涉及的知识点有:待定系数法可求抛物线的解析式,待定系数法求直线的解析式,二次函数的性质,轴对称的性质,两点间的距离公式,中点坐标公式,以及方程思想的应用,综合性较强,有一定的难度.

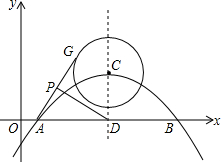 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
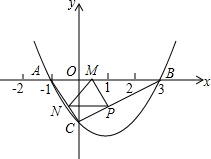 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,连接AC、BC,A、C两点的坐标分别为A(-1,0),C(0,-$\sqrt{3}$),且当x=-2和x=4时二次函数的函数值y相等.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,连接AC、BC,A、C两点的坐标分别为A(-1,0),C(0,-$\sqrt{3}$),且当x=-2和x=4时二次函数的函数值y相等.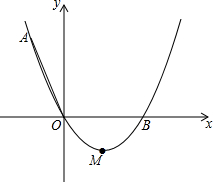 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=4,∠AOB=120°.
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=4,∠AOB=120°. 如图所示,抛物线y=x2+bx+c与直线y=x-1交于A、B两点,点A的纵坐标为-4,点B在y轴上,直线AB与x轴交于点F,点P是线段AB下方的抛物线上一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
如图所示,抛物线y=x2+bx+c与直线y=x-1交于A、B两点,点A的纵坐标为-4,点B在y轴上,直线AB与x轴交于点F,点P是线段AB下方的抛物线上一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.