题目内容
某商场推销一种书包,进价为30元,在试销中发现这种书包每天的销售量P(个)与每个书包销售价x(元)满足一次函数关系式.当定价为35元时,每天销售30个;定价为40元时,每天销售20个.
(1)求P关于x的函数关系式;
(2)如果要保证商场每天销售这种书包获利200元,求书包的销售单价应定为多少元?
(1)求P关于x的函数关系式;
(2)如果要保证商场每天销售这种书包获利200元,求书包的销售单价应定为多少元?
考点:一元二次方程的应用,一次函数的应用
专题:销售问题
分析:(1)根据待定系数法可求P关于x的函数关系式.
(2)设此时书包的单价是x元,根据题意找出涨价和销售量的关系,然后根据利润200元列方程求解.
(2)设此时书包的单价是x元,根据题意找出涨价和销售量的关系,然后根据利润200元列方程求解.
解答:解:(1)设P=kx+b,
根据题意得:
,
解得:
,
则P关于x的函数关系式P=-2x+100,
(2)设此时书包的销售单价应定为x元.
则P(x-30)=200,
(-2x+100)(x-30)=200,
解得x=40.
故书包的销售单价应定为40元.
根据题意得:
|
解得:
|
则P关于x的函数关系式P=-2x+100,
(2)设此时书包的销售单价应定为x元.
则P(x-30)=200,
(-2x+100)(x-30)=200,
解得x=40.
故书包的销售单价应定为40元.
点评:本题考查一元二次方程的应用、一次函数的应用和理解题意的能力,关键看出涨价和销售量的关系,然后根据利润列方程求解.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图,在?ABCD中,增加一个条件四边形ABCD就成为矩形,这个条件是( )
如图,在?ABCD中,增加一个条件四边形ABCD就成为矩形,这个条件是( )| A、AB=CD |
| B、∠A+∠C=180° |
| C、BD=2AB |
| D、AC⊥BD |
下列各组线段,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、5cm,6cm,10cm |
| C、1cm,1cm,3cm |
| D、3cm,4cm,8cm |
 如图,在周长为12的菱形ABCD中,∠BAC=60°,则对角线AC的长为( )
如图,在周长为12的菱形ABCD中,∠BAC=60°,则对角线AC的长为( )| A、3 | B、6 | C、9 | D、12 |
 如图,在△ABC中,AB=AC=10,BC=12,AH⊥BC于H,点P从点B出发沿射线BC以每秒3个单位长度的速度运动,点Q从点C出发沿CA边以每秒2个单位长度的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交AH所在直线于点E.若P、Q两点同时出发,当点Q运动到点A时,P、Q两点停止运动,设运动时间为t秒(t>0).
如图,在△ABC中,AB=AC=10,BC=12,AH⊥BC于H,点P从点B出发沿射线BC以每秒3个单位长度的速度运动,点Q从点C出发沿CA边以每秒2个单位长度的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交AH所在直线于点E.若P、Q两点同时出发,当点Q运动到点A时,P、Q两点停止运动,设运动时间为t秒(t>0).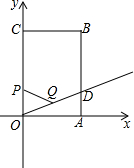 已知如图,矩形OABC在平面直角坐标系中,OA=
已知如图,矩形OABC在平面直角坐标系中,OA=