题目内容
8.为了促进旅游业的发展,某市新建一座景观桥.桥的拱肋ADB可视为抛物线的一部分,桥面AB可视为水平线段,桥面与拱肋用垂直于桥面的杆状景观灯连接,拱肋的跨度AB为40米,桥拱的最大高度CD为16米(不考虑灯杆和拱肋的粗细),求与CD的距离为5米的景观灯杆MN的高度.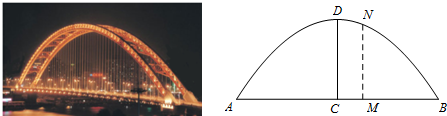
分析 以AB所在直线为x轴、CD所在直线为y轴建立坐标系,可设该抛物线的解析式为y=ax2+16,将点B坐标代入求得抛物线解析式,再求当x=5时y的值即可.
解答 解:建立如图所示平面直角坐标系,
设抛物线表达式为y=ax2+16,
由题意可知,B的坐标为(20,0)
∴400a+16=0
∴$a=-\frac{1}{25}$
∴$y=-\frac{1}{25}{x^2}+16$,
∴当x=5时,y=15.
答:与CD距离为5米的景观灯杆MN的高度为15米.
点评 本题考查了二次函数的应用,涉及了待定系数法求抛物线解析式的知识,建立合适的平面直角坐标系是解题的关键.

练习册系列答案
相关题目
18.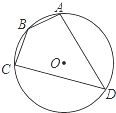 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | 4π |
19.本学期的四次数学单元练习中,甲、乙两位同学的平均成绩一样,方差分别为1.0,0.6,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 甲乙两人的成绩一样稳定 | ||
| C. | 乙比甲的成绩稳定 | D. | 无法确定谁的成绩更稳定 |
16.某班5名同学在一周内参加家务劳动的时间如表所示,则关于“劳动时间”的这组数据的中位数是4.
| 劳动时间(小时) | 2 | 3 | 4 | 5 |
| 人数 | 1 | 1 | 2 | 1 |
13. 如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )| A. | 梦 | B. | 我 | C. | 中 | D. | 国 |
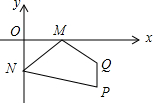 如图,点P的坐标是(3,-2),点Q的坐标是(3,-1),点M是x轴上一个动点,点N是y轴上的一个动点,则四边形MNPQ周长的最小值是2$\sqrt{13}$+1.
如图,点P的坐标是(3,-2),点Q的坐标是(3,-1),点M是x轴上一个动点,点N是y轴上的一个动点,则四边形MNPQ周长的最小值是2$\sqrt{13}$+1.