题目内容
(本题满分8分)已知一次函数 的图象经过点
的图象经过点 ,且与正比例函数
,且与正比例函数 的图象相交于点
的图象相交于点 .
.

(1)求一次函数 的表达式;
的表达式;
(2)在同一坐标系中,画出这两个函数的图象,并求这两条直线与 轴围成的三角形的面积.
轴围成的三角形的面积.
(1) ;
;
(2)如图,直线 、
、 即为所画,两条直线与
即为所画,两条直线与 轴所围的三角形面积为
轴所围的三角形面积为

【解析】
试题分析:(1)要求一次函数解析式,需知道两个点的坐标,已知条件中有一个点,还需求出与正比例函数的交点,将交点代入正比例函数解析式即可求得;(2)两点确定一条直线,取两个点作出相应的直线即可,要求两直线与 轴所围三角形面积,可根据图像先求得各个交点,再分别求三角形的底和高,应用公式即可求解.
轴所围三角形面积,可根据图像先求得各个交点,再分别求三角形的底和高,应用公式即可求解.
试题解析:(1) 在
在 图像上
图像上  即交点为
即交点为
将 、
、 代入
代入 ,得
,得  解得
解得
 一次函数的表达式为
一次函数的表达式为 ;
;
(2)如图,直线 、
、 即为所画.
即为所画.

由图知,两条直线与 轴所围的三角形为
轴所围的三角形为 ,且
,且 ,
,


 两条直线与
两条直线与 轴所围的三角形面积为
轴所围的三角形面积为 .
.
考点:1.待定系数法求一次函数解析式;2.作一次函数的图像;3.函数图像的综合应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 y-16y= .
y-16y= . 地骑车出发,10时30分到达
地骑车出发,10时30分到达 地.小李开车从
地.小李开车从 后,要恢复原价,则应提价( ) .
后,要恢复原价,则应提价( ) . B.
B. D.
D.
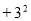 与
与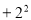 B.
B.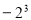 与
与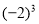
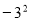 与
与 D.
D.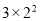 与
与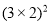
 轴翻折,再向右平移
轴翻折,再向右平移 个单位称为
个单位称为 次变换.如图,已知正方形
次变换.如图,已知正方形 的顶点
的顶点 、
、 的坐标分别是
的坐标分别是 、
、 ,把正方形
,把正方形 次这样的变换得到正方形
次这样的变换得到正方形 ,则
,则 的对应点
的对应点 的坐标是 .
的坐标是 .
 ,
, 相交于点
相交于点 ,
, ,请你补充一个条件,使得
,请你补充一个条件,使得 ≌
≌ ,你补充的条件是 .
,你补充的条件是 .
 ÷
÷  ;
; .
.