题目内容
2.观察下列单项式:3a2、5a5、7a10、9a17、11a26…它们是按一定规律排列的,那么这列式子的第n个单项式是(2n+1)a${\;}^{{n}^{2}+1}$..分析 找出前3项的规律,然后通过后面几项验证,找出规律得到答案.
解答 解:3a2=(2×1+1)a${\;}^{{1}^{2}+1}$,
5a5=(2×2+1)a${\;}^{{2}^{2}+1}$,
7a10=(2×3+1)a${\;}^{{3}^{2}+1}$,
…
第n个单项式是:(2n+1)a${\;}^{{n}^{2}+1}$.
故答案为:(2n+1)a${\;}^{{n}^{2}+1}$.
点评 本题是根据给出的数据寻找规律,解题的关键是找出前几项的规律,然后几项验证,最后得到规律.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
14.设x是实数,y=|x-1|+|x+1|,下列结论正确的是( )
| A. | y没有最小值 | |
| B. | 只有一个x使y取到最小值 | |
| C. | 有有限多个x(不止一个)使y取到最小值 | |
| D. | 有无穷多个x使y取到最小值 |
 (1)根据图中的规律,写出a7;
(1)根据图中的规律,写出a7; 如图△ABC的周长是30cm,把△ABC的边AC对折,使点C和点A重合,折痕是DE交BC和AC于D点和E点,连接AD,若EC=4cm,△ABD的周长是22cm.
如图△ABC的周长是30cm,把△ABC的边AC对折,使点C和点A重合,折痕是DE交BC和AC于D点和E点,连接AD,若EC=4cm,△ABD的周长是22cm.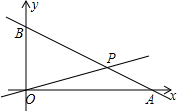 在如图所示的直角坐标系中,O为原点,直线y=-$\frac{1}{2}$x+8与x轴、y轴分别交于A、B两点,设直线OP与线段AB相交于P点,且$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,试求点P的坐标.
在如图所示的直角坐标系中,O为原点,直线y=-$\frac{1}{2}$x+8与x轴、y轴分别交于A、B两点,设直线OP与线段AB相交于P点,且$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,试求点P的坐标.