题目内容
9.观察下面一列数,探求其规律$\frac{1}{2}$,-$\frac{2}{3}$,$\frac{3}{4}$,-$\frac{4}{5}$,$\frac{5}{6}$,-$\frac{6}{7}$,…(1)这一列数属于有理数中的哪一类?
(2)写出第7,8,9项的三个数;
(3)第2013个数是什么?
(4)如果这一列数无限排列下去,与哪两个越来越接近?
分析 (1)这列数属于有理数中的分数;
(2)这列数正负相间,奇数为负,偶数为正,分母比分子大1,于是第7,8,9项的三个数为$\frac{7}{8}$,-$\frac{8}{9}$,$\frac{9}{10}$;
(3)根据(2)可知,第2013个数是$\frac{2013}{2014}$;
(4)如果这一列数无限排列下去,与±1越来越接近.
解答 解:(1)属于有理数中的分数;
(2)第7,8,9项的三个数分别是:$\frac{7}{8}$,-$\frac{8}{9}$,$\frac{9}{10}$;
(3)第2013个数是$\frac{2013}{2014}$;
(4)这一列数无限排列下去,与±1越来越接近.
点评 此题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是得到这列数正负相间,即奇数项是负数,偶数项为正,且第n个数的分子是n,分母是n+.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
1.二次函数y=ax2+x+c2(a≠0)的图象可能是( )
| A. | 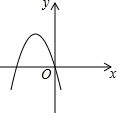 | B. | 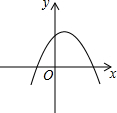 | C. | 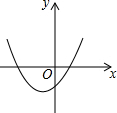 | D. | 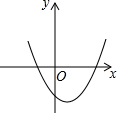 |
