题目内容
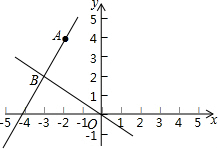 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-| 2 |
| 3 |
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数y=-
| 2 |
| 3 |
(3)直接写出关于x的不等式-
| 2 |
| 3 |
考点:两条直线相交或平行问题,一次函数图象与几何变换,一次函数与一元一次不等式
专题:
分析:(1)先确定B的坐标,然后根据待定系数法求解析式;
(2)先求得C的坐标,然后根据题意求得平移后的直线的解析式,把C的坐标代入平移后的直线的解析式,即可求得M的值;
(3)根据图象即可求得不等式-
x>kx+b的解集.
(2)先求得C的坐标,然后根据题意求得平移后的直线的解析式,把C的坐标代入平移后的直线的解析式,即可求得M的值;
(3)根据图象即可求得不等式-
| 2 |
| 3 |
解答:解:(1)∵正比例函数y=-
x的图象经过点B(a,2).
∴2=-
a,解得,a=-3,
∴B(-3,2),
∵一次函数y=kx+b的图象经过点A(-2,4),B(-3,2),
∴
,解得,
,
∴一次函数y=kx+b的解析式为y=2x+8;
(2)∵一次函数y=2x+8的图象与x轴交于点C,
∴C(-4,0),
∵正比例函数y=-
x的图象向下平移m(m>0)个单位长度后经过点C,
∴平移后的函数的解析式为y=-
x-m,
∴0=-
×(-4)-m,解得,m=
;
(3)∵B(-3,2),
∴根据图象可知-
x>kx+b的解集为:x<-3.
| 2 |
| 3 |
∴2=-
| 2 |
| 3 |
∴B(-3,2),
∵一次函数y=kx+b的图象经过点A(-2,4),B(-3,2),
∴
|
|
∴一次函数y=kx+b的解析式为y=2x+8;
(2)∵一次函数y=2x+8的图象与x轴交于点C,
∴C(-4,0),
∵正比例函数y=-
| 2 |
| 3 |
∴平移后的函数的解析式为y=-
| 2 |
| 3 |
∴0=-
| 2 |
| 3 |
| 8 |
| 3 |
(3)∵B(-3,2),
∴根据图象可知-
| 2 |
| 3 |
点评:本题考查了两条直线相交或平行的问题,应用的知识点有:待定系数法,直线上点的坐标特征,直线的平移,一次函数和一元一次不等式的关系.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
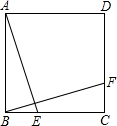 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=( )
如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=( )| A、60° | B、90° |
| C、120° | D、45° |
已知A、B、C、D依次是直线AD上的4个不同点,则下列说法正确的是( )
| A、线段AD与线段BC是两条相同线段 |
| B、直线AD与直线BC是两条不同直线 |
| C、射线AB于射线AD是两条相同射线 |
| D、射线BC于射线BD是两条里不同射线 |
 如图,下午2点30分时,时钟的分针与时针所成角的度数为( )
如图,下午2点30分时,时钟的分针与时针所成角的度数为( )| A、90° | B、120° |
| C、105° | D、135° |
 如图,在△DEF中,EF=2,DE=4,∠DEF=120°,求DF的长.
如图,在△DEF中,EF=2,DE=4,∠DEF=120°,求DF的长.