题目内容
 如图,在△DEF中,EF=2,DE=4,∠DEF=120°,求DF的长.
如图,在△DEF中,EF=2,DE=4,∠DEF=120°,求DF的长.考点:解直角三角形,勾股定理
专题:
分析:过F作FG⊥DE,交DE的延长与点G,由∠DEF=120°,可得∠FEG=60°,由FG⊥EG,可得∠EFG=30°,然后由30°角所对的直角边等于斜边的一半,可求EG的值进而可求DG的值,然后在Rt△EFG中由勾股定理可求FG的值,在Rt△DFG中由勾股定理可求DF的值.
解答:解:过F作FG⊥DE,交DE的延长与点G,可得Rt△EFG和Rt△DFG,

∵∠DEF=120°,
∴∠FEG=60°
∵在Rt△EFG中,∠FEG=60°,
∴∠EFG=30°,
∴EG=
EF,
∵EF=2,
∴EG=1,
∴DG=DE+EG=5,
在Rt△EFG中,
由勾股定理得:FG=
=
,
在Rt△DFG中,
由勾股定理得:DF=
=
=2
.

∵∠DEF=120°,
∴∠FEG=60°
∵在Rt△EFG中,∠FEG=60°,
∴∠EFG=30°,
∴EG=
| 1 |
| 2 |
∵EF=2,
∴EG=1,
∴DG=DE+EG=5,
在Rt△EFG中,
| DG2+FG2 |
由勾股定理得:FG=
| EF2-EG2 |
| 3 |
在Rt△DFG中,
由勾股定理得:DF=
| DG2+FG2 |
| 28 |
| 7 |
点评:此题考查了直角三角形的有关性质,涉及勾股定理及30°角所对的直角边等于斜边的一半等知识.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
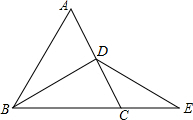 如图,若△ABC是等边三角形,AB=6,BD是∠ABC的平分线,延长BC到E,使CE=CD,则BE=( )
如图,若△ABC是等边三角形,AB=6,BD是∠ABC的平分线,延长BC到E,使CE=CD,则BE=( )| A、7 | B、8 | C、9 | D、10 |
若∠A的余角是它的7倍,则∠A的度数等于( )
| A、11°2′5″ |
| B、11°15′ |
| C、11°25′ |
| D、11°12′30″ |
下列调查,比较适合采用普查方式的是( )
| A、调查海尔某种型号数字电视机的使用寿命 |
| B、调查中央电视台《开讲了》栏目的收视率 |
| C、调查全国中学生的体重 |
| D、调查你们班同学的身高 |
若函数y=x2-6x+c的最小值是4,则c=( )
| A、4 | B、9 | C、5 | D、13 |
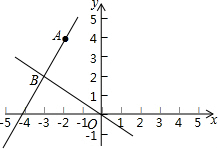 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-