题目内容
2.在△ABC中,AD平分∠BAC,AB=AC+CD,则∠B:∠C=1:2.分析 根据题意画出图形,AB上截取AC′=AC,依据SAS证明△ACD≌△AC′D,由全等三角形的性质可知DC=C′D,∠C=∠AC′D.根据题意可知BC′=C′D,于是得到∠B=∠BDC′由三角形外角的性质可知∠B+∠BDC′=∠AC′D,故此2∠B=∠C.
解答 解:如图所示:在AB上截取AC′=AC.
∵AD平分∠BAC,
∴∠CAD=∠C′AD.
∵在△ACD和△AC′D中
$\left\{\begin{array}{l}{AC=AC′}\\{∠CAD=∠C′AD}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AC′D.
∴DC=C′D,∠C=∠AC′D.
∵AB=AC+CD,AC′=AC,
∴BC′=C′D.
∴∠B=∠BDC′.
∵∠B+∠BDC′=∠AC′D,
∴2∠B=∠C.
∴∠B:∠C=1:2.
故答案为:1:2.
点评 本题主要考查的是全等三角形的性质和判定,等腰三角形的性质和判定、三角形的外角的性质,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
 用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )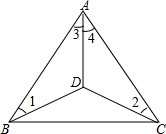 已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.
已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.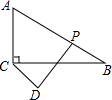 如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2.
如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|=a-c.
已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|=a-c.