Question

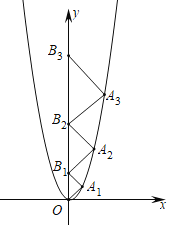
【题目】二次函数y＝2x2的图象如图所示，坐标原点O，点B1，B2，B3在y轴的正半轴上，点A1，A2，A3在二次函数y＝2x2位于第一象限的图象上，若△A1OB1，△A2B1B2，△A3B2B3都为等腰直角三角形，且点A1，A2，A3均为直角顶点，则点A3的坐标是_____．

Answer 1

【答案】（，）．

【解析】

过A1，A2，A3作y轴的垂线，垂足分别为A、B、C，设OB1=a，B1B2=b，B2B3=c，则AA1=a，BA2=b，CA3=c，再根据等腰直角三角形的性质，分别表示A1，A2，A3的纵坐标，逐步代入抛物线y=2x2中，求a、b、c的值，得出点A3的坐标．

分别过A1，A2，A3作y轴的垂线，垂足分别为A、B、C，

设OB1＝a，B1B2＝b，B2B3＝c，则AA1＝a，BA2＝b，CA3＝c，

在等腰直角△OB1A1中，A1（a，a），代入y＝2x2中，得a＝2（a）2，解得a＝1，

∴A1（，），

在等腰直角△B1A2B2中，A2（b，1+b），代入y＝2x2中，得1+b＝2（b）2，解得b＝2，

∴A2（1，2），

在等腰直角△B2A3B3中，A3（c，3+），代入y＝2x2中，得3+c＝2（c）2，解得c＝3，

∴A3（，），

故答案为：（，）．