题目内容
12.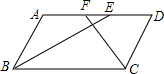 如图,在?ABCD中,AB=5,AD=8,BE平分∠ABC,交AD于点E,CF平分∠BCD,交AD于点F.
如图,在?ABCD中,AB=5,AD=8,BE平分∠ABC,交AD于点E,CF平分∠BCD,交AD于点F.(1)求EF;
(2)你能发现BE与CF有什么关系吗?并证明之.
分析 (1)根据平行四边形的性质可知∠AEB=∠EBC,又因为BE平分∠ABC,所以∠ABE=∠EBC,则∠ABE=∠AEB,则AB=AE=5,同理可证FD=5,即可得出结论;
(2)由平行四边形的性质和角平分线定义得出∠BMC=90°,即可得出结论.
解答 解:(1)∵四边形ABCD是平行四边形,
∴∠AEB=∠EBC,AB∥CD,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
则∠ABE=∠AEB,
∴AB=AE=5,
同理可证:DF=DC=AB=5,
则EF=AE+FD-AD=5+5-8=2;
(2)BE⊥CF,理由如下:
如图所示:
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵BE平分∠ABC,CF平分∠BCD,
∴∠CBE=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠BCD,
∴∠CBE+∠BCF=$\frac{1}{2}$×180°=90°,
∴∠BMC=90°,
∴BE⊥CF.
点评 本题主要考查了平行四边形的性质,等腰三角形的判定;在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
2.|-6|=( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | ±6 |
2.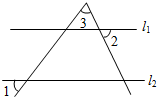 如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )
如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )
 如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )
如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
 已知A(0,8),B(6,0),在坐标轴上取一点P,使三角形ABP为等腰三角形,求P点的坐标.
已知A(0,8),B(6,0),在坐标轴上取一点P,使三角形ABP为等腰三角形,求P点的坐标.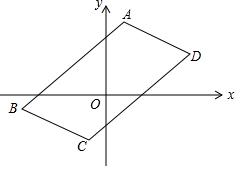 图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点
图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点 画出函数y=$\frac{6}{x}$(x>0)的图象.
画出函数y=$\frac{6}{x}$(x>0)的图象.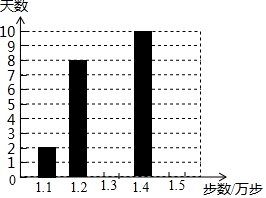 乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).